Question

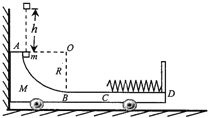
【题目】如图所示，光滑水平地面上停放着一辆质量为M的小车，小车的左侧靠在竖直墙壁上，半径为R的四分之一光滑圆弧轨道AB的最低点B与水平轨道BD平滑相接，小车的右端固定有一个轻质弹簧，弹簧左端自然伸长至C点，水平轨道BC段粗糙，CD段光滑．现有一可视为质点的物块从A点正上方h=R处无初速度下落，物块质量为m，恰好落入小车沿圆轨道滑动，然后沿水平轨道滑行，与弹簧相接触并压缩弹簧，最后又返回到B点相对于车静止．已知M=3m，物块与水平轨道BC间的动摩擦因数为μ，不考虑空气阻力和物块落入圆弧轨道时的能量损失．求

（1）物块下落后由A滑至B处时，对轨道的压力大小；

（2）压缩弹簧过程中，弹簧所具有的最大弹性势能．

Answer 1

【答案】(1)5mg (2)

【解析】

（1）物块从静止释放至B的过程中小车不动，对物体由机械能守恒定律有：

mg（h+R）=…①

解得：vB=2…②

在B处时，由牛顿第二定律有：N-mg=m…③

解得：N=5mg…④

（2）物块滑上水平轨道至B与小车相对静止的过程中，对系统由动量守恒和能量守恒有：

mvB=（m+M）v共…⑤

…⑥

解得：L= ⑦

物块滑上水平轨道至将弹簧压缩至最短的过程中，对系统由动量守恒和能量守恒有：

mvB=（m+M）v′共…⑧

…⑨

解得：Epm=

答：（1）物块下落后由A滑至B处时，对轨道的压力大小为5mg；

（2）压缩弹簧过程中，弹簧所具有的最大弹性势能为．