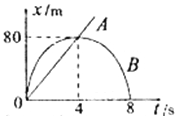
��Ŀ����
����Ŀ���ס���ͬʱ��A���ɾ�ֹ��������ֱ��AB�˶��������Լ��ٶ�a1���ȼ����˶�����һ��ʱ����Լ��ٶ�a2���ȼ����˶�������B���ٶ�Ϊv0����һֱ�Լ��ٶ�a���ȼ����˶�������B���ٶ�ҲΪv0����֪a1��a����(�� )
A. a2��a
B. ��A��B������ʱ����
C. ����AB����һ��ʱ���ٶ�һ�������ҵ��ٶ�
D. ����AB��ijһ��ʱ�����ٶȿ���С���ҵ��ٶ�
���𰸡�BC
��������
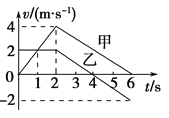
��v-tͼ������ͼ��ʾ����ɫб�ߴ�����v-tͼ��ɫб�ߴ����ҵ�v-tͼ���ҵ�λ����ȣ����ҵĸ��Ե�v-tͼ���߶������Ƕ�Ӧ��ʱ���ᡢ�ٶ�����Χ�ɵļ���ͼ�������ȡ��Ƚ�����ͼ1��ͼ2֪������ͬ��ĩ��v��ǰ���£�Ҫʹ���ҵ����ն�Bʱλ����ȣ�ͼ�������ȣ����ҵ�v-tͼ���߶ε��ն˱����ڼ�v-tͼ���߶��ն˵��ұߣ���ͼ2���Ƿ��������v-tͼ�������ҵ�v-tͼ���߶ε��ն˱ض��ڼ�v-tͼ���߶��ն˵��ұߣ��ʱ���t����t������һ���ȵ���B������a2��a�Ĵ�С����ȷ������A������B��ȷ����ͼ2����v-tͼ���ϼ��ҵĹ�ͬʱ�������ѡһʱ��t����t��Ӧ���ٶ��ᣨ��ɫ���ߣ������ٶ��������v-tͼ���߶εĽ���ȽϿɵõ����ۣ���������ͬ��ʱ�̣����У�v����v������C��ȷ��D����ѡBC��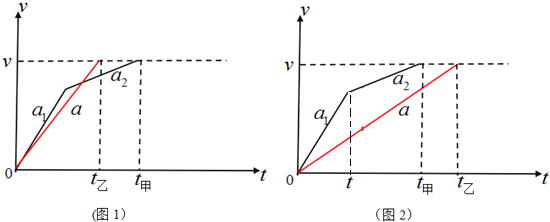

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�