题目内容
7. 在光滑水平面上,有一转轴垂直于此平面,交点O的上方h处固定一细绳,绳的另一端连接一质量为m的小球B,绳长l>h,小球可随转轴转动在光滑水平面上做匀速圆周运动,如图所示.要使小球不离开水平面,转轴转速的最大值是( )
在光滑水平面上,有一转轴垂直于此平面,交点O的上方h处固定一细绳,绳的另一端连接一质量为m的小球B,绳长l>h,小球可随转轴转动在光滑水平面上做匀速圆周运动,如图所示.要使小球不离开水平面,转轴转速的最大值是( )| A. | $\frac{1}{2π}$$\sqrt{\frac{g}{h}}$ | B. | π$\sqrt{gh}$ | C. | $\frac{1}{2π}$$\sqrt{\frac{g}{l}}$ | D. | $\frac{1}{2π}$$\sqrt{\frac{l}{g}}$ |
分析 要使球不离开水平面,临界情况是对水平面的压力为零,靠拉力和重力的合力提供向心力,结合牛顿第二定律求出转动轴的最大角速度,从而得出转速的最大值.
解答 解:当小球对水平面的压力为零时,有:Tcosθ=mg,Tsinθ=mlsinθω2,
解得最大角速度为:ω=$\sqrt{\frac{g}{lcosθ}}$=$\sqrt{\frac{g}{h}}$,
则最大转速为:n=$\frac{ω}{2π}=\frac{1}{2π}\sqrt{\frac{g}{h}}$,故A正确,B、C、D错误.
故选:A.
点评 解决本题的关键抓住小球不脱离水平面的临界状态,结合牛顿第二定律进行求解,知道角速度与转速的关系.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
2. 如图所示,一个立方体与一倾角为θ的斜面紧靠在一起,一个小球共立方体的顶端O点水平抛出,小球落到斜面上后反弹,反弹速度仍然水平,设球与斜面间的碰撞为弹性碰撞(入射速度与反弹速度与斜面的夹角相等).则小球从抛出到落到斜面上所用的时间为( )
如图所示,一个立方体与一倾角为θ的斜面紧靠在一起,一个小球共立方体的顶端O点水平抛出,小球落到斜面上后反弹,反弹速度仍然水平,设球与斜面间的碰撞为弹性碰撞(入射速度与反弹速度与斜面的夹角相等).则小球从抛出到落到斜面上所用的时间为( )
 如图所示,一个立方体与一倾角为θ的斜面紧靠在一起,一个小球共立方体的顶端O点水平抛出,小球落到斜面上后反弹,反弹速度仍然水平,设球与斜面间的碰撞为弹性碰撞(入射速度与反弹速度与斜面的夹角相等).则小球从抛出到落到斜面上所用的时间为( )
如图所示,一个立方体与一倾角为θ的斜面紧靠在一起,一个小球共立方体的顶端O点水平抛出,小球落到斜面上后反弹,反弹速度仍然水平,设球与斜面间的碰撞为弹性碰撞(入射速度与反弹速度与斜面的夹角相等).则小球从抛出到落到斜面上所用的时间为( )| A. | $\frac{2{v}_{0}tanθ}{g}$ | B. | $\frac{{v}_{0}tanθ}{g}$ | C. | $\frac{{v}_{0}tan2θ}{g}$ | D. | $\frac{2{v}_{0}tan2θ}{g}$ |
12. 在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图1所示.产生的交变电动势的图象如图2所示,则( )
在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图1所示.产生的交变电动势的图象如图2所示,则( )
 在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图1所示.产生的交变电动势的图象如图2所示,则( )
在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图1所示.产生的交变电动势的图象如图2所示,则( )| A. | t=0.005s时线框的磁通量变化率为零 | |
| B. | 线框产生的交变电动势有效值为311V | |
| C. | t=0.01s时线框平面与磁场垂直 | |
| D. | 线框产生的交变电动势频率为100HZ |
19.以水平面为零势能面,则小球水平抛出时重力势能等于动能的2倍,那么在抛体运动过程中,当其动能和势能相等时,水平速度和竖直速度之比为( )
| A. | $\sqrt{3}$:1 | B. | 1:1 | C. | 1:$\sqrt{2}$ | D. | $\sqrt{2}$:1 |
 质量为M的小车,如图所示,上面站着一个质量为m的人,以v0的速度在光滑的水平面上前进.现在人用相对于小车为u的速度水平向后跳出后,车速变为多大?
质量为M的小车,如图所示,上面站着一个质量为m的人,以v0的速度在光滑的水平面上前进.现在人用相对于小车为u的速度水平向后跳出后,车速变为多大?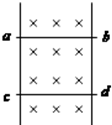 竖直放置的平行光滑金属导轨,其电阻不计,磁场方向如图所示,磁感应强度B=0.5T,有两根相同的导体棒ab及cd,长0.2m,电阻0.1Ω,重0.1N,现用力向上拉动导体ab,使之匀速上升(与导轨接触良好).此时cd恰好静止不动,求:
竖直放置的平行光滑金属导轨,其电阻不计,磁场方向如图所示,磁感应强度B=0.5T,有两根相同的导体棒ab及cd,长0.2m,电阻0.1Ω,重0.1N,现用力向上拉动导体ab,使之匀速上升(与导轨接触良好).此时cd恰好静止不动,求: