题目内容
如图所示,一高h=0.45m、长L=0.5m、质量为M=6kg的木板车B静止于光滑水平面上,小物体A(可视为质点)质量为m=3kg,用长为H =0.8m的轻绳把质量m0=1kg的小钢球悬挂在O点.将轻绳拉直至水平位置后静止释放小球,与小物体A发生碰撞后以原来速度的一半反弹.已知A和B间的动摩擦因数μ=0.2,不计空气阻力.重力加速度取g =10m/s2.
(1) 求小钢球与小物体A碰撞前的速度v1的大小;
(2) 求小物体A与小钢球碰撞后获得的速度v2的大小;
(3) 小物体A能否从木板车B的右端飞出?如果能,试计算小物体A落地与木板车B右端的水平距离s的大小.

(1)小钢球从最高点摆至与A碰撞的过程中,由机械能守恒定律有:
m0gH=![]() mv12 (2分)
mv12 (2分)
得:v1=4m/s (2分)
(2)设小物体A被小钢球碰撞后的速度为v2,A与小钢球碰撞的过程动量守恒,有:
m0v1=-m0![]() +mv2 (2分)
+mv2 (2分)
得:v2=2m/s (2分)
(3)设小物体A运动至木板车B右端时的速度为v3,木板车B的速度为v4.A与B发生相对运动的过程中,动量守恒,有
mv2=mv3+Mv4 (3分)
A与B发生相对运动的过程中,根据能量守恒定律,有:
μmgL=![]() mv22-(
mv22-(![]() mv32+
mv32+![]() Mv42) (3分)
Mv42) (3分)
以上两式联立解得:v3=![]() m/s,v4=
m/s,v4=![]() m/s (2分)
m/s (2分)
因为v3>v4,说明小物体A能从木板车B的右端飞出. (2分)
小物体A从木板车右端飞出后做平抛运动,根据平抛运动的规律,在竖直方向上,
h=![]() gt2 (2分)
gt2 (2分)
得A作平抛运动的时间t=0.3s (2分)
小物体A落地与木板车B右端的水平距离s=(v3-v4)t=0.3m (2分)

 如图所示,一高h=0.8m的光滑曲形槽底端B与水平传带平滑相接,传送带的运行速度为v0=6m/s,长为L=0.9m,滑块与传送带间的动摩擦因数μ=0.5,DEF为固定于竖直平面内的一段内壁光滑的中空方形细管,EF段被弯成以O为圆心、半径R=1.0m的一小段圆弧,管的D端弯成与水平传带C端平滑相接,O点位于地面,OF连线竖直.一质量为M=0.2kg的物块a从曲面槽顶端A点无初速释放,经B点滑到传送带上,过后滑块被传送带送入管DEF,管内顶端F点放置一质量为m=0.2kg的物块b,.已知a、b两物块均可视为质点,a、b横截面略小于管中空部分的横截面,重力加速度g取l0m/s2.求:
如图所示,一高h=0.8m的光滑曲形槽底端B与水平传带平滑相接,传送带的运行速度为v0=6m/s,长为L=0.9m,滑块与传送带间的动摩擦因数μ=0.5,DEF为固定于竖直平面内的一段内壁光滑的中空方形细管,EF段被弯成以O为圆心、半径R=1.0m的一小段圆弧,管的D端弯成与水平传带C端平滑相接,O点位于地面,OF连线竖直.一质量为M=0.2kg的物块a从曲面槽顶端A点无初速释放,经B点滑到传送带上,过后滑块被传送带送入管DEF,管内顶端F点放置一质量为m=0.2kg的物块b,.已知a、b两物块均可视为质点,a、b横截面略小于管中空部分的横截面,重力加速度g取l0m/s2.求: 如图所示,有一根长L1=0.5m的木棍,悬挂在某房顶上,它自由下落时经过一高为L2=1.5m的窗口,通过窗口所用的时间为t=0.2s,不计空气阻力.求窗口上沿离木棍的悬点O的距离h?(取g=10m/s2)
如图所示,有一根长L1=0.5m的木棍,悬挂在某房顶上,它自由下落时经过一高为L2=1.5m的窗口,通过窗口所用的时间为t=0.2s,不计空气阻力.求窗口上沿离木棍的悬点O的距离h?(取g=10m/s2)
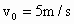 的速度在平面上向右运动,求小球从A点运动到地面所需的时间.(平面与斜面均光滑,取
的速度在平面上向右运动,求小球从A点运动到地面所需的时间.(平面与斜面均光滑,取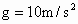 )
)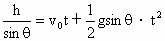 ,由此可求得落地的时间t.
,由此可求得落地的时间t.