题目内容
如图所示,质量为mA=2kg的木板A静止放在光滑水平面上,一质量为mB=1kg的小物块B从固定在地面上的光滑弧形轨道距木板A上表面某一高H处由静止开始滑下,以某一初速度v0滑上A的左端,当A向右运动的位移为L=0.5m时,B的速度为vB=4m/s,此时A的右端与固定竖直挡板相距x,已知木板A足够长(保证B始终不从A上滑出),A与挡板碰撞无机械能损失,A、B之间动摩擦因数为μ=0.2,g取10m/s2
(1)求B滑上A的左端时的初速度值v0及静止滑下时距木板A上表面的高度H
(2)当x满足什么条件时,A与竖直挡板只能发生一次碰撞

(1)求B滑上A的左端时的初速度值v0及静止滑下时距木板A上表面的高度H
(2)当x满足什么条件时,A与竖直挡板只能发生一次碰撞

分析:(1)A、B组成的系统动量守恒,由动量守恒定律可以求出A的初速度,由机械能守恒定律或动能定理可以求出物体A下滑的高度.
(2)A、B组成的系统动量守恒,当碰撞之后系统动量向左或为零时,A只于挡板碰撞一次,由动量守恒定律、动能定理即可正确解题.
(2)A、B组成的系统动量守恒,当碰撞之后系统动量向左或为零时,A只于挡板碰撞一次,由动量守恒定律、动能定理即可正确解题.
解答:解:(1)假设B的速度从v0减为vB=4m/s时,A一直加速到vA,
以A为研究对象,由动能定理 μmBgL=
mA
-0 ①,
代入数据解得vA=1m/s<vB,故假设成立;
在A向右运动位移L=0.5m的过程中,A、B系统动量守恒,
由动量守恒定律得:mBv0=mAvA+mBvB ②,
联立①②解得 v0=6m/s;
B下滑过程中机械能守恒,由机械能守恒定律得:
mB
=mBgH,解得 H=1.8m;
(2)设A、B与挡板碰前瞬间的速度分别为vA1、vB1,
由动量守恒定律mBv0=mAvA1+mBvB1 ③,
以A为研究对象,由动能定理 μmBg(L+x)=
mA
-0,④,
由于A与挡板碰撞无机械能损失,故A与挡板碰后瞬间的速度大小为vA1,
碰后系统总动量不再向右时,A与竖直挡板只能发生一次碰撞,
即mA
≥mBvB1 ⑤,联立③④⑤解得 x≥0.625m;
答:(1)B滑上A的左端时的初速度值v0为6m/s,静止滑下时距木板A上表面的高度为1.8m;
(2)当 x≥0.625m时,A与竖直挡板只能发生一次碰撞.
以A为研究对象,由动能定理 μmBgL=
| 1 |
| 2 |
| v | 2 A |
代入数据解得vA=1m/s<vB,故假设成立;
在A向右运动位移L=0.5m的过程中,A、B系统动量守恒,
由动量守恒定律得:mBv0=mAvA+mBvB ②,
联立①②解得 v0=6m/s;
B下滑过程中机械能守恒,由机械能守恒定律得:
| 1 |
| 2 |
| v | 2 0 |
(2)设A、B与挡板碰前瞬间的速度分别为vA1、vB1,
由动量守恒定律mBv0=mAvA1+mBvB1 ③,
以A为研究对象,由动能定理 μmBg(L+x)=
| 1 |
| 2 |
| v | 2 A1 |
由于A与挡板碰撞无机械能损失,故A与挡板碰后瞬间的速度大小为vA1,
碰后系统总动量不再向右时,A与竖直挡板只能发生一次碰撞,
即mA
| v | A1 |
答:(1)B滑上A的左端时的初速度值v0为6m/s,静止滑下时距木板A上表面的高度为1.8m;
(2)当 x≥0.625m时,A与竖直挡板只能发生一次碰撞.
点评:本题考查了动量守恒定律、动能定理的应用,本题第(2)小题是本题的难点,知道A与挡板碰撞一次的条件是正确解题的前提与关键.

练习册系列答案
相关题目
 如图所示,质量为mA=2kg的木板A静止在光滑水平面上,一质量为mB=1kg的小物块B以某一初速度vo从A的左端向右运动,当A向右运动的路程为L=0.5m时,B的速度为vB=8m/s,此时A的右端与固定竖直挡板相距x.已知木板A足够长(保证B始终不从A上掉下来),A与挡板碰撞无机械能损失,A、B之间的动摩擦因数为μ=0.2,g取10m/s2
如图所示,质量为mA=2kg的木板A静止在光滑水平面上,一质量为mB=1kg的小物块B以某一初速度vo从A的左端向右运动,当A向右运动的路程为L=0.5m时,B的速度为vB=8m/s,此时A的右端与固定竖直挡板相距x.已知木板A足够长(保证B始终不从A上掉下来),A与挡板碰撞无机械能损失,A、B之间的动摩擦因数为μ=0.2,g取10m/s2 (2013?许昌三模)如图所示,质量为mA=2kg的木块A静止在光滑水平面上.一质量为mB=1kg的木块B以某一初速度v0=5m/s沿水平方向向右运动,与A碰撞后都向右运动.木块A与挡板碰撞后立即反弹(设木块A与挡板碰撞过程无机械能损失).后来木块A与B发生二次碰撞,碰后A、B同向运动,速度大小分别为0.9m/s、1.2m/s.求:
(2013?许昌三模)如图所示,质量为mA=2kg的木块A静止在光滑水平面上.一质量为mB=1kg的木块B以某一初速度v0=5m/s沿水平方向向右运动,与A碰撞后都向右运动.木块A与挡板碰撞后立即反弹(设木块A与挡板碰撞过程无机械能损失).后来木块A与B发生二次碰撞,碰后A、B同向运动,速度大小分别为0.9m/s、1.2m/s.求:
 如图所示,质量为mA的物块A用不可伸长的细线吊着,在A的下方用弹簧连着质量为mB的物块B,开始时静止不动.现在B上施加一个竖直向下的力F,缓慢拉动B使之向下运动一段距离后静止(弹簧始终在弹性限度内),希望撤去力F后,B向上运动并能顶起A,则力F的最小值是( )
如图所示,质量为mA的物块A用不可伸长的细线吊着,在A的下方用弹簧连着质量为mB的物块B,开始时静止不动.现在B上施加一个竖直向下的力F,缓慢拉动B使之向下运动一段距离后静止(弹簧始终在弹性限度内),希望撤去力F后,B向上运动并能顶起A,则力F的最小值是( )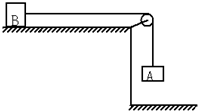 如图所示,质量为mA=1kg、mB=3kg的两个物体A和B.,用跨过定滑轮的细绳相连.用力把B压在水平桌面上.使A离地面的高度为H=2.0m,且桌面上方细绳与桌面平行.现撤去压B的外力.使A、B从静止开始运动,A着地后不反弹,在运动过程中B始终碰不到滑轮.B与水平桌面间的动摩擦因数为μ=0.2,不汁滑轮与轴间、绳子的摩擦、不计空气阻力及细绳和滑轮的质量,取g=10m/s2.求:
如图所示,质量为mA=1kg、mB=3kg的两个物体A和B.,用跨过定滑轮的细绳相连.用力把B压在水平桌面上.使A离地面的高度为H=2.0m,且桌面上方细绳与桌面平行.现撤去压B的外力.使A、B从静止开始运动,A着地后不反弹,在运动过程中B始终碰不到滑轮.B与水平桌面间的动摩擦因数为μ=0.2,不汁滑轮与轴间、绳子的摩擦、不计空气阻力及细绳和滑轮的质量,取g=10m/s2.求: