Question

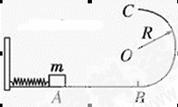
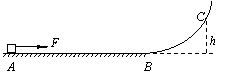
如图所示，半径为R的光滑圆形轨道在B点与水平轨道AB相切，水平轨道AB在A点与光滑弧形轨道CA相切，轨道CA、AB与圆形轨道都在同一竖直平面内．现让一质量为m的滑块（可视为质点）从弧形轨道上高为h处由静止释放．设滑块与AB轨道的动摩擦因数为μ，AB轨道的长度为x₀．为使滑块在进入圆形轨道后能够不脱离轨道而运动，滑块释放的高度h应满足什么条件?（假设B处的缺口不影响滑块进入圆轨道和在圆轨道的上运动）

Answer 1

滑块不脱离轨道的条件是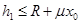：或者。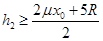

解析试题分析：滑块不脱离轨道有两种情况，第一是滑块进入圆形轨道后上升的最大高度不超过圆形轨道的半径R；第二种是滑块能通过轨道的轨道的最高点，由功能原理可得：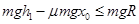
① ②
若滑块恰能通过圆形轨道的最高点，则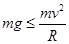：③，由①式解得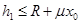：④；联立②③可得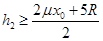：⑤；即滑块不脱离轨道的条件是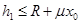：或者。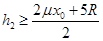
考点：牛顿定律及能量守恒定律。