题目内容
3.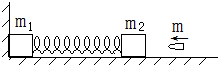 如图所示,固定在轻质弹簧两端质量分别是m1=m、m2=$\frac{3}{4}$m的两个物体置于光滑水平面上,m1靠在光滑竖直墙上,现有一颗m3=$\frac{1}{4}$m的子弹水平射入m2中,使弹簧压缩最短时具有的弹性势能为E,然后m1和m2都将向右运动,试求:
如图所示,固定在轻质弹簧两端质量分别是m1=m、m2=$\frac{3}{4}$m的两个物体置于光滑水平面上,m1靠在光滑竖直墙上,现有一颗m3=$\frac{1}{4}$m的子弹水平射入m2中,使弹簧压缩最短时具有的弹性势能为E,然后m1和m2都将向右运动,试求:(1)子弹入射m2前的速度;
(2)m1离开墙后运动过程中弹簧具有的最大弹性势能;
(3)m1离开墙后运动过程中m1具有的最大速度.
分析 (1)根据能量守恒求出子弹射入木块2后的速度,结合动量守恒定律求出子弹入射m2前的速度;
(2)m1离开墙后,当弹簧伸长到最长时,弹性势能最大,此时两者速度相等,根据动量守恒定律和能量守恒定律求出最大弹性势能;
(3)当弹簧恢复原长时,m1具有的最大速度.根据动量守恒定律和能量守恒定律求出m1具有的最大速度.
解答 解:(1)对子弹射入木块后到弹簧压缩量最大的过程中,运用能量守恒得:E=$\frac{1}{2}({m}_{2}+{m}_{3}){v}^{2}$,
解得子弹射入木块为:$v=\sqrt{\frac{2E}{{m}_{2}+{m}_{3}}}=\sqrt{\frac{2E}{m}}$,
子弹射入木块的过程中动量守恒,规定子弹初速度的方向为正方向,根据动量守恒守恒得:m3v1=(m2+m3)v,
解得:${v}_{1}=4\sqrt{\frac{2E}{m}}$.
(2)m1离开墙后,当弹簧伸长到最长时,弹性势能最大,此时两者速度相等.规定向右为正方向,有:(m2+m3)v=(m1+m2+m3)v2,
解得:${v}_{2}=\frac{v}{2}=\frac{1}{2}\sqrt{\frac{2E}{m}}$.
根据能量守恒得,最大弹性势能为:${E}_{p}=\frac{1}{2}({m}_{2}+{m}_{3}){v}^{2}-\frac{1}{2}({m}_{1}+{m}_{2}+{m}_{3}){{v}_{2}}^{2}$=$\frac{E}{2}$.
(3)当弹簧恢复原长时,m1具有的最大速度.规定向右为正方向,
根据动量守恒有:(m1+m2+m3)v2=m1v1′+(m2+m3)v′,
根据能量守恒有:$\frac{1}{2}({m}_{2}+{m}_{3}){v}^{2}=\frac{1}{2}{m}_{1}{v}_{1}{′}^{2}+$$\frac{1}{2}({m}_{2}+{m}_{3})v{′}^{2}$,
联立两式解得:v1′=v=$\sqrt{\frac{2E}{m}}$.
答:(1)子弹入射m2前的速度为$4\sqrt{\frac{2E}{m}}$;
(2)m1离开墙后运动过程中弹簧具有的最大弹性势能为$\frac{E}{2}$;
(3)m1离开墙后运动过程中m1具有的最大速度为$\sqrt{\frac{2E}{m}}$.
点评 本题是含有弹簧的类型,对于子弹打击过程,要明确研究对象,确定哪些物体参与作用,运用动量守恒能量守恒进行求解即可.

 阅读快车系列答案
阅读快车系列答案①摩擦力对物体一定做负功
②摩擦力对物体可以做正功,也可以做负功,还可以不做功
③在同样时间内,作用力和反作用力的功大小不一定相等,但正负号一定相反
④在同样时间内,作用力和反作用力的功大小不一定相等,正负号也不一定相反.
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
| A. | 线速度大小保持不变,方向保持不变 | |
| B. | 线速度大小保持不变,方向时刻改变 | |
| C. | 向心加速度大小保持不变,方向保持不变 | |
| D. | 向心力的大小保持不变,方向保持不变 |
| A. | 在某时刻质点受到的合力可能为零 | |
| B. | 速度可能不变 | |
| C. | 在某一点的速度方向是该点曲线的切线方向 | |
| D. | 加速度一定发生改变 |
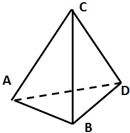 如图所示,正四面体所有棱长都相等长度为a,A、B、C、D是其四个顶点,现在B、D两点分别固定电量均为q的正负点电荷,静电力常量为k,下列说法正确的是( )
如图所示,正四面体所有棱长都相等长度为a,A、B、C、D是其四个顶点,现在B、D两点分别固定电量均为q的正负点电荷,静电力常量为k,下列说法正确的是( )| A. | C点的场强大小为$\sqrt{3}$$\frac{kq}{{a}^{2}}$ | |
| B. | A、C两点的场强方向相同 | |
| C. | A、C两点电势相同 | |
| D. | 将一正电荷从A点沿直线移动到C点,电场力先做正功后做负功 |