题目内容
8.某质点做曲线运动时( )| A. | 在某时刻质点受到的合力可能为零 | |
| B. | 速度可能不变 | |
| C. | 在某一点的速度方向是该点曲线的切线方向 | |
| D. | 加速度一定发生改变 |
分析 曲线运动的速度方向沿曲线的切线方向,故速度一定变化,加速度一定不为零,合力不为零;速度的方向与合外力的方向必定不在同一条直线上.
解答 解:A、曲线运动的速度方向沿曲线的切线方向,时刻改变,一定是变速运动,故加速度一定不为零,合力也就一定不为零,故A错误;
B、曲线运动的速度方向沿曲线的切线方向,时刻改变,一定是变速运动,故B错误;
C、曲线运动的速度方向沿曲线的切线方向,故C正确;
D、曲线运动的加速度可以不变,如平抛运动的加速度恒为g,故D错误;
故选:C
点评 本题关键掌握曲线运动的条件,速度方向一定变,大小不一定变.加速度可以是恒定的也可以是变化的,但速度一定是变化的.

练习册系列答案
相关题目
19.据报道,“嫦娥一号”预计在2007年发射,“嫦娥一号”将在距离月球为h高处绕月球做匀速圆周运动,已知月球半径为R,月球表面的重力加速度为g0.“嫦娥一号”环绕月球运行的周期为( )
| A. | $\frac{{4{π^2}R}}{g_0}$ | B. | $\frac{{4{π^2}(R+h)}}{g_0}$ | C. | $\frac{2πh}{R}\sqrt{\frac{h}{g_0}}$ | D. | $\frac{2π(R+h)}{R}\sqrt{\frac{R+h}{g_0}}$ |
16. 在高速公路的拐弯处,路面造得外高内低,即当车向右拐弯时,司机左侧的路面比右侧的要高一些,路面与水平面间的夹角为θ,设拐弯路段是半径为R的圆弧,要使车速为v时车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零,θ应满足( )
在高速公路的拐弯处,路面造得外高内低,即当车向右拐弯时,司机左侧的路面比右侧的要高一些,路面与水平面间的夹角为θ,设拐弯路段是半径为R的圆弧,要使车速为v时车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零,θ应满足( )
 在高速公路的拐弯处,路面造得外高内低,即当车向右拐弯时,司机左侧的路面比右侧的要高一些,路面与水平面间的夹角为θ,设拐弯路段是半径为R的圆弧,要使车速为v时车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零,θ应满足( )
在高速公路的拐弯处,路面造得外高内低,即当车向右拐弯时,司机左侧的路面比右侧的要高一些,路面与水平面间的夹角为θ,设拐弯路段是半径为R的圆弧,要使车速为v时车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零,θ应满足( )| A. | sinθ=$\frac{{v}^{2}}{Rg}$ | B. | tanθ=$\frac{{v}^{2}}{Rg}$ | C. | sin2θ=$\frac{2{v}^{2}}{Rg}$ | D. | cotθ=$\frac{{v}^{2}}{Rg}$ |
13.下列关于曲线运动的说法正确的是( )
| A. | 可以是匀速运动 | B. | 一定是变速运动 | ||
| C. | 一定是匀变速运动 | D. | 加速度可能恒为零 |
20.两个半径为r的,由同种材料制成的均匀球体,球心之间的距离是100r,它们之间万有引力大小是F,则F与r的关系是( )
| A. | F与r2成反比 | B. | F与r2成正比 | C. | F与r3成正比 | D. | F与r4成正比 |
17.质量为3kg的物体,从高45m处自由落下(g取10m/s2),那么在下落的过程中( )
| A. | 前2s内重力做功的功率为300W | B. | 前2s内重力做功的功率为675 W | ||
| C. | 第2s末重力做功的功率为600W | D. | 第2s末重力做功的功率为900W |
14.在“探究弹性势能的表达式”的实验中,为了计算弹簧弹力所做的功,把拉伸弹簧的过程分为很多小段,拉力为每小段可以认为是恒力,用各小段做的功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”.下面实例中应用到这一思想方法的是( )
| A. | 根据加速度的定义a=$\frac{△v}{△t}$,当△t非常小,$\frac{△v}{△t}$就可以表示物体在t时刻的瞬时加速度 | |
| B. | 在探究加速度、力和质量三者之间关系时,先保持质量不变,研究加速度与力的关系,再保持力不变,研究加速度与质量的关系 | |
| C. | 在推导匀变速直线运动的位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加 | |
| D. | 在不需要考虑物体本身的大小和形状时,用点来代替物体,即质点 |
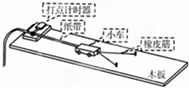 探究力对原来静止的物体做的功与物体获得的速度的关系,实验装置如图所示,实验主要过程如下:
探究力对原来静止的物体做的功与物体获得的速度的关系,实验装置如图所示,实验主要过程如下: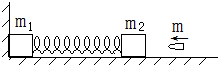 如图所示,固定在轻质弹簧两端质量分别是m1=m、m2=$\frac{3}{4}$m的两个物体置于光滑水平面上,m1靠在光滑竖直墙上,现有一颗m3=$\frac{1}{4}$m的子弹水平射入m2中,使弹簧压缩最短时具有的弹性势能为E,然后m1和m2都将向右运动,试求:
如图所示,固定在轻质弹簧两端质量分别是m1=m、m2=$\frac{3}{4}$m的两个物体置于光滑水平面上,m1靠在光滑竖直墙上,现有一颗m3=$\frac{1}{4}$m的子弹水平射入m2中,使弹簧压缩最短时具有的弹性势能为E,然后m1和m2都将向右运动,试求: