题目内容
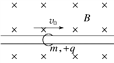
【题目】如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,a、b间的电场强度为E,今有一带正电的微粒从a板下边缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝进入bc区域,bc区域的宽度也为d,所加电场的场强大小为E,方向竖直向上,磁感应强度方向垂直纸面向里,磁场磁感应强度大小等于![]() ,重力加速度为g,则下列关于微粒运动的说法正确的是( )
,重力加速度为g,则下列关于微粒运动的说法正确的是( )
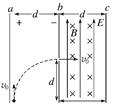
A. 微粒在ab区域的运动时间为![]()
B. 微粒在bc区域中做匀速圆周运动,圆周半径r=2d
C. 微粒在bc区域中做匀速圆周运动,运动时间为![]()
D. 微粒在ab、bc区域中运动的总时间为![]()
【答案】ABD
【解析】将粒子在电场中的运动沿水平和竖直方向正交分解,水平分运动为初速度为零的匀加速运动,竖直分运动为末速度为零的匀减速运动,根据运动学公式,有水平方向: ![]() ,
, ![]() ,竖直方向:
,竖直方向: ![]() ,解得:
,解得: ![]() ,
, ![]() ,故A正确;粒子在复合场中运动时,由于电场力与重力平衡,故粒子做匀速圆周运动,洛伦兹力提供向心力,有:
,故A正确;粒子在复合场中运动时,由于电场力与重力平衡,故粒子做匀速圆周运动,洛伦兹力提供向心力,有: ![]() ,解得:
,解得: ![]() ,联立解得:r=2d,故B错误;由于r=2d,画出轨迹,如图
,联立解得:r=2d,故B错误;由于r=2d,画出轨迹,如图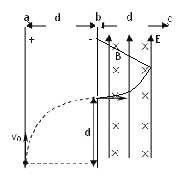
由几何关系,得到回旋角度为30°,故在复合场中的运动时间为: ![]() ,故C正确;粒子在电场中运动时间为:
,故C正确;粒子在电场中运动时间为: 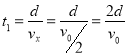 ,故粒子在ab、bc区域中运动的总时间为:
,故粒子在ab、bc区域中运动的总时间为: ![]() 故D正确。所以ABD正确,C错误。
故D正确。所以ABD正确,C错误。

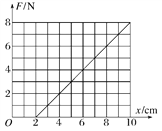
【题目】在“探究弹簧弹力大小与伸长量的关系”实验中,甲、乙两位同学选用不同的橡皮绳代替弹簧,为测量橡皮绳的劲度系数,他们在橡皮绳下端面依次逐个挂下钩码(每个钩码的质量均为m=0.1kg,取g=10m/s2),并记录绳下端的坐标X加(下标i表示挂在绳下端钩码个数).然后逐个拿下钩码,同样记录绳下端面的坐标X减,绳下端面坐标的值Xi=(X加+X减)/2的数据如下表:
挂在橡皮绳下端的钩码个数 | 橡皮绳下端的坐标(X/mm) | |
甲 | 乙 | |
1 | 216.5 | 216.5 |
2 | 246.7 | 232.0 |
3 | 284.0 | 246.5 |
4 | 335.0 | 264.2 |
5 | 394.5 | 281.3 |
6 | 462.0 | 301.0 |
(1)同一橡皮绳的X加_______X减(大于、小于或等于);
(2)_______同学的数据更符合实验要求(甲或乙);
(3)选择乙同学的数据用作图法求出该橡皮绳的劲度系数______k(N/m).