题目内容
5.实验装置如图1所示,让重锤拖动纸带自由下落,通过打点计时器打下一系列的点,对纸带上的点迹进行测量、分析和计算处理,即可验证重锤下落过程机械能是否守恒.
(1)下面列举了验证机械能守恒定律实验的几个操作步骤:
A.按照图示的装置安装实验器材;
B.将打点计时器接到学生电源输出电压为6V的“直流输出”挡;
C.用天平测出重锤的质量;
D.先释放纸带,然后立刻接通电源,打出一条纸带;
E.测量纸带上某些点间的距离;
F.根据测量的结果计算重锤下落过程中减少的重力势能与增加的动能的关系.
其中没有必要进行的步骤是C,操作不当的步骤是BD.
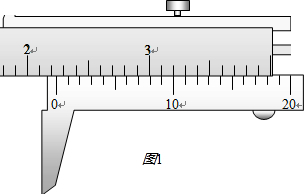
(2)如图2所示是某次实验打出的一条纸带,选取纸带上连续的五个点A、B、C、D、E,测出各点之间的距离分别为:x0=6.79cm,x1=7.19cm,x2=7.58cm,x3=7.97cm,x4=8.36cm所用电源的频率f=50Hz,重锺的质量m=1.00kg,查得当地重力加速度g=9.80m/s2.
①重锤由O点运动到D点,重力势能的减少量等于8.40J,动能的增加量等于8.32J (保留三位有效数字),实验结论:在实验误差允许的范围内,重锤下落过程机械能守恒.
②重锤从O点运动到D点的过程中受到的平均阻力约为0.05 N.
分析 (1)解决实验问题首先要掌握该实验原理,了解实验的仪器、操作步骤和数据处理以及注意事项,只有这样才能明确每步操作的具体含义.
(2)根据重力做功和重力势能的关系可以求出重力势能的减小量;匀变速直线运动中中间时刻的瞬时速度等于该过程中的平均速度,由此求出C点的速度,进一步可以求出重锤动能的增加量;利用匀变速直线运动的推理△x=aT2可以求出重锤下落的加速度大小也可以利用机械能守恒定律的表达式求出加速度的大小.
解答 解:(1)B:将打点计时器接到电源的“交流输出”上,故B错误,操作不当.
C:因为我们是比较mgh、$\frac{1}{2}$mv2的大小关系,故m可约去比较,不需要用天平,故C没有必要.
D、应该先接通电源再释放纸带,故D错误,操作不当.
故答案为:C,BD.
(2)①重力势能的减小量等于重力做功大小,故有:
△EP=mg(x0+x1+x2+x3)=1×9.8×(6.19+7.19+7.58+7.97)×10-2J=8.40 J
由题意可知,各个点之间的时间间隔为T=$\frac{1}{f}$=0.02s,
匀变速直线运动中中间时刻的瞬时速度等于该过程中的平均速度,由此可以求出D点的速度大小为:
vD=$\frac{{x}_{3}+{x}_{4}}{2T}$=$\frac{(7.97+8.36)×1{0}^{-2}}{0.04}$m/s=4.08m/s,
所以动能的增量为:
△EK=$\frac{1}{2}$m${{v}_{D}}^{2}$-0=$\frac{1}{2}×1×4.0{8}^{2}$=8.32 J
实验结论:在实验误差允许的范围内,重锤下落过程机械能守恒
②重锤下落时做匀加速运动,
采用逐差法求解加速度.
x3-x1=2a1T2,
x4-x2=2a2T2,
a=$\frac{1}{2}$(a1+a2)
代入数据解得a=9.75m/s2.
根据牛顿第二定律得F合=mg-f=ma
f=mg-ma=1×(9.80-9.75)N=0.05 N
故答案为:(1)C,BD
(2)①8.40 J; 8.32 J; 在实验误差允许的范围内,重锤下落过程机械能守恒 ②0.05
点评 解答实验问题的关键是明确实验原理、实验目的,了解具体操作,要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.

 如图所示,用细线将一小球悬挂在光滑墙壁上,小球的质量为m,若增加细线的长度,以下说法中正确的是( )
如图所示,用细线将一小球悬挂在光滑墙壁上,小球的质量为m,若增加细线的长度,以下说法中正确的是( )| A. | 细线的拉力变大 | B. | 细线的拉力变小 | ||
| C. | 墙壁对球的支持力变小 | D. | 墙壁对球的支持力变大 |
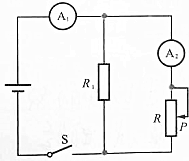
| A. | A1、A2的示数同时增大,同时减小 | |
| B. | A1的示数增加时A2的示数减小,A1的示数减小时A2的示数增大 | |
| C. | A1的示数总大于A2的示数 | |
| D. | A1、A2示数的大小关系无法确定 |
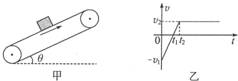 已知一足够长的传送带与水平面的倾角为θ,以恒定的速度顺时针转动.某时刻在传送带适当的位置放上具有一定初速度质量为m的小物块,如图甲所示.以此时为t=0时刻,小物块的速度随时间的变化关系如图乙所示(甲图中取沿传送带向上的方向为正方向,乙图中v1>v2),则下列判断正确的是( )
已知一足够长的传送带与水平面的倾角为θ,以恒定的速度顺时针转动.某时刻在传送带适当的位置放上具有一定初速度质量为m的小物块,如图甲所示.以此时为t=0时刻,小物块的速度随时间的变化关系如图乙所示(甲图中取沿传送带向上的方向为正方向,乙图中v1>v2),则下列判断正确的是( )| A. | 0~t1内传送带对小物块做正功 | |
| B. | 小物块与传送带间的动摩擦因数μ>tanθ | |
| C. | 0~t2内传送带对小物块做功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv12 | |
| D. | 0~t2内小物块对传送带间因摩擦数产生的热量大于小物块动能的减少量 |
 如图为一个质点在水平面上沿直线运动的位移时间图象,规定向右为正方向,那么请根据图中信息回答以下问题:
如图为一个质点在水平面上沿直线运动的位移时间图象,规定向右为正方向,那么请根据图中信息回答以下问题: