题目内容
12．
如图所示，用细线将一小球悬挂在光滑墙壁上，小球的质量为m，若增加细线的长度，以下说法中正确的是（ ）| A． | 细线的拉力变大 | B． | 细线的拉力变小 | ||
| C． | 墙壁对球的支持力变小 | D． | 墙壁对球的支持力变大 |
分析 对球受力分析，根据共点力平衡得到绳子拉力和墙壁对球的弹力的表达式，再进行分析．
解答 
解：小球的受力如图所示．根据平衡条件得：
Tcosθ=G
Tsinθ=N
则得：N=Gtanθ
T=$\frac{G}{cosθ}$
若增加细线的长度，θ减小，tanθ减小，cosθ增大，则得T和N均变小，即细线的拉力变小，墙壁对球的支持力变小．故BC正确．
故选：BC
点评 本题根据平衡条件得到力的表达式，再分析其变化情况，是一种函数法，也可以采用图解法分析．
练习册系列答案
阅读快车系列答案
相关题目
2．
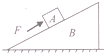如图所示，水平地面上有一斜面B，上面放一物块A，一平行斜面向上的力F作用于物体A上．在力F变大的过程中，A、B始终保持静止，则以下说法中正确的是（ ）
如图所示，水平地面上有一斜面B，上面放一物块A，一平行斜面向上的力F作用于物体A上．在力F变大的过程中，A、B始终保持静止，则以下说法中正确的是（ ）| A． | 物体A受到的支持力一定变小 | B． | 物体A受到的摩擦力一定变大 | ||
| C． | 斜面B受到地面的支持力一定变小 | D． | 斜面B受到地面的摩擦力一定不变 |
3．关于加速度，下列说法正确的是（ ）
| A． | 速度变化越大，加速度一定越大 | |
| B． | 加速度就是增加的速度 | |
| C． | 速度变化越快，加速度一定越大 | |
| D． | 单位时间内速度变化越大，加速度一定越大 |
20．
在探索弹力和弹簧伸长量之间的关系的实验中，弹簧受到拉力作用后会伸长，平衡时弹簧产生的弹力和它受到的拉力大小相等，研究弹簧受到的拉力大小和弹簧伸长量之间的关系，就可以得到弹力大小和弹簧伸长量之间的关系．某同学实验时所用的弹簧，不受外力作用时长为20.0cm，将弹簧竖直悬挂后在下面挂上砝码，弹簧产生的弹力大小F（数值上等于所挂砝码的重力）和弹簧总长度上之间的关系如下表所示：
（1）根据上述实验数据在如图上建立坐标系，作出F和弹簧伸长量x之间的关系图线．
（2）你所得到的图线的特点是：过原点的倾斜直线．
在探索弹力和弹簧伸长量之间的关系的实验中，弹簧受到拉力作用后会伸长，平衡时弹簧产生的弹力和它受到的拉力大小相等，研究弹簧受到的拉力大小和弹簧伸长量之间的关系，就可以得到弹力大小和弹簧伸长量之间的关系．某同学实验时所用的弹簧，不受外力作用时长为20.0cm，将弹簧竖直悬挂后在下面挂上砝码，弹簧产生的弹力大小F（数值上等于所挂砝码的重力）和弹簧总长度上之间的关系如下表所示：| 弹簧的总长度L/cm | 20.9 | 22.0 | 23.1 | 24.0 | 24.9 | 26.1 | 27.0 | 27.9 |
| 弹簧的弹力F/N | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
（2）你所得到的图线的特点是：过原点的倾斜直线．
7．
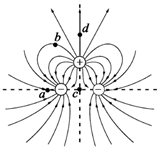两个相同的负电荷和一个正电荷附近的电场线分布如图所示，c是两负电荷连线的中点，d点在正电荷的正上方，c、d到正电荷的距离相等，则（ ）
两个相同的负电荷和一个正电荷附近的电场线分布如图所示，c是两负电荷连线的中点，d点在正电荷的正上方，c、d到正电荷的距离相等，则（ ）| A． | a点的电场强度比b点的大 | B． | a点的电势比b点的高 | ||
| C． | c点的电场强度比d点的小 | D． | c点的电势比d点的低 |
17．一物体在某行星的赤道上，随该行星自转时受到的该行星对他的万有引力是它重力的1.04倍，已知该行星自转的周期为T，行星的半径为R，把该行星看成一个球体，则该行星的第一宇宙速度为（ ）
| A． | $\frac{2πR}{T}$ | B． | $\frac{4πR}{T}$ | C． | $\frac{10πR}{T}$ | D． | $\frac{25πR}{T}$ |
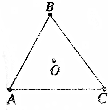在绝缘的光滑水平桌面上，有三个带电小球A、B、C，带电量均为Q（正电），每个小球的质量均为m，各自位置分别位于边长为L的等边三角形的三个顶点，如图所示．假设本题中的带电小球均被视为点电荷，不计彼此间的万有引力作用．
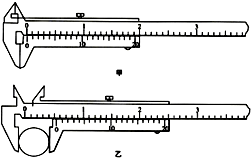某同学利用游标卡尺测量一金属圆筒的外径，图甲为该游标卡尺校零时的示数，图乙为测量金属圆筒外径时，示数．如图甲所示，读数为0.15mm，如图乙所示，读数为5.35mm，所测金属筒外径为5.20mm．