题目内容
5. 如图甲所示,光滑金属导轨MN、PQ所在平面与水平面成θ角,M、P两端接一电阻R,整个装置处于方向垂直导轨平面上的匀强磁场中.t=0时对金属棒施加一平行于导轨的外力F,使金属棒ab由静止开始沿导轨向上运动,导轨电阻忽略不计.已知通过电阻R的感应电流I随时间t变化的关系如图乙所示.下列关于棒运动速度v、外力F、流过R的电量q以及闭合回路中磁通量的变化率$\frac{△φ}{△t}$随时间变化的图象正确的是( )
如图甲所示,光滑金属导轨MN、PQ所在平面与水平面成θ角,M、P两端接一电阻R,整个装置处于方向垂直导轨平面上的匀强磁场中.t=0时对金属棒施加一平行于导轨的外力F,使金属棒ab由静止开始沿导轨向上运动,导轨电阻忽略不计.已知通过电阻R的感应电流I随时间t变化的关系如图乙所示.下列关于棒运动速度v、外力F、流过R的电量q以及闭合回路中磁通量的变化率$\frac{△φ}{△t}$随时间变化的图象正确的是( )| A. |  | B. |  | C. | 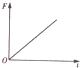 | D. | 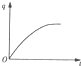 |
分析 由题可知,金属棒由静止开始沿导轨向上做匀加速运动,回路中的感应电流与时间成正比,说明感应电动势也是随时间均匀增大的,明确各个图象的物理意义,结合产生感应电流的特点即可正确求解.
解答 解:A、而E=Blv,所以v=$\frac{k(R+r)}{Bl}$,v-t图象是一条过原点斜率大于零的直线,说明了导体棒做的是初速度为零的匀加速直线运动,即v=at;故A错误;
B、根据如图乙所示的I-t图象可知I=kt,其中k为比例系数,由闭合电路欧姆定律可得:I=$\frac{E}{R+r}$=kt
可推出:E=kt(R+r)而E=$\frac{△Φ}{△t}$,
所以有:$\frac{△Φ}{△t}$=kt(R+r)图象是一条过原点斜率大于零的直线;故B正确;
C、对导体棒在沿导轨方向列出动力学方程F-BIl-mgsinθ=ma,而I=$\frac{Blv}{R+r}$,v=at,
得到F=$\frac{{B}^{2}{l}^{2}a}{R+r}$t+m(a+gsinθ),可见F-t图象是一条斜率大于零且与速度轴正半轴有交点的直线;故C错误.
D、q=$\overline{I}t$=$\frac{△Φ}{R+r}$=$\frac{Bla}{2(R+r)}{t}^{2}$,q-t图象是一条开口向上的抛物线,故D错误;
故选:B.
点评 此题考查以电磁感应问题中的图象为命题情境考查学生推理能力和应用数学处理物理问题的能力;对于图象问题一定弄清楚两坐标轴的含义,尤其注意斜率、截距的含义,对于复杂的图象可以通过写出两坐标轴所代表物理量的函数表达式进行分析

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
15. 如图所示,为赤道上随地球自转的物体A、赤道上空的近地卫星B和地球的同步卫星C的运动示意图,若它们的运动都可视为匀速圆周运动,则比较三个物体的运动情况,以下判断正确的是( )
如图所示,为赤道上随地球自转的物体A、赤道上空的近地卫星B和地球的同步卫星C的运动示意图,若它们的运动都可视为匀速圆周运动,则比较三个物体的运动情况,以下判断正确的是( )
 如图所示,为赤道上随地球自转的物体A、赤道上空的近地卫星B和地球的同步卫星C的运动示意图,若它们的运动都可视为匀速圆周运动,则比较三个物体的运动情况,以下判断正确的是( )
如图所示,为赤道上随地球自转的物体A、赤道上空的近地卫星B和地球的同步卫星C的运动示意图,若它们的运动都可视为匀速圆周运动,则比较三个物体的运动情况,以下判断正确的是( )| A. | 三者角速度的大小关系为ωA=ωC<ωB | |
| B. | 三者向心加速度大小关系为aA>aB>aC | |
| C. | 三者的周期关系为TA=TC<TB | |
| D. | 三者线速度的大小关系为vA>vB>vC |
13.物体做平抛运动时,在任意相同时间间隔内,速度的变化量( )
| A. | 大小不同,方向不同 | B. | 大小相同,方向不同 | ||
| C. | 大小不同,方向相同 | D. | 大小相同,方向相同 |
20.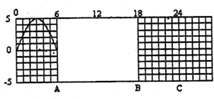 如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm,在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是( )
如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm,在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是( )
 如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm,在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是( )
如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm,在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是( )| A. | 3.6cm/s | B. | 4.8cm/s | C. | 6 cm/s | D. | 7.2 cm/s |
15.X射线( )
| A. | 不是电磁波 | B. | 具有反射和折射的特性 | ||
| C. | 只能在介质中传播 | D. | 不能发生干涉和衍射 |
 一圆筒形汽缸水平放置在水平地面上,内壁光滑,下端密封,上端封闭但留有一抽气孔.汽缸内下部被活塞封住一定量的理想气体,气体温度为300K,开始时,活塞上方 的压强p0=1×105Pa,活塞下方气体的体积为100cm3,活塞上方气体的体积为260cm3,活塞重力产生的压强是0.5×105Pa,将活塞上方缓慢抽成真空并密封,整个抽气过程中缸内气体温度始终保持不变.然后将密封的气体缓慢加热.求:
一圆筒形汽缸水平放置在水平地面上,内壁光滑,下端密封,上端封闭但留有一抽气孔.汽缸内下部被活塞封住一定量的理想气体,气体温度为300K,开始时,活塞上方 的压强p0=1×105Pa,活塞下方气体的体积为100cm3,活塞上方气体的体积为260cm3,活塞重力产生的压强是0.5×105Pa,将活塞上方缓慢抽成真空并密封,整个抽气过程中缸内气体温度始终保持不变.然后将密封的气体缓慢加热.求: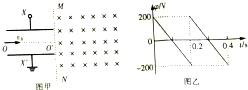 示波管中有两个偏转电极,其中一个电极XX′上可以接入仪器自身产生的锯齿形电压,叫扫描电压.如图甲所示,已知XX′极板长L=0.2$\sqrt{3}$m,板间距d=0.2m,在金属板右端竖直边界MN的右侧有一区域足够大的匀强磁场B=5×10-3T,方向垂直纸面向里.现将X′极板接地,X极板上电势φ随时间变化规律如图乙所示.有带正电的粒子流以速度v0=1×105m/s,沿水平中线OO′连续射入电场中,粒子的比荷$\frac{q}{m}$=1×108C/kg,重力忽略不计,在每个粒子通过电场的极短时间内,电场可视为匀强电场.(设两板外无电场,结果可用根式表示)求:
示波管中有两个偏转电极,其中一个电极XX′上可以接入仪器自身产生的锯齿形电压,叫扫描电压.如图甲所示,已知XX′极板长L=0.2$\sqrt{3}$m,板间距d=0.2m,在金属板右端竖直边界MN的右侧有一区域足够大的匀强磁场B=5×10-3T,方向垂直纸面向里.现将X′极板接地,X极板上电势φ随时间变化规律如图乙所示.有带正电的粒子流以速度v0=1×105m/s,沿水平中线OO′连续射入电场中,粒子的比荷$\frac{q}{m}$=1×108C/kg,重力忽略不计,在每个粒子通过电场的极短时间内,电场可视为匀强电场.(设两板外无电场,结果可用根式表示)求: 如图电容器AB,电容器UAB=+U,两极板的距离为d,质量为m的小球,电量为-q.从静止从B板运动A板.
如图电容器AB,电容器UAB=+U,两极板的距离为d,质量为m的小球,电量为-q.从静止从B板运动A板.