题目内容
14.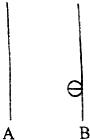 如图电容器AB,电容器UAB=+U,两极板的距离为d,质量为m的小球,电量为-q.从静止从B板运动A板.
如图电容器AB,电容器UAB=+U,两极板的距离为d,质量为m的小球,电量为-q.从静止从B板运动A板.(1)小球加速度;
(2)运动A板时的速度.
分析 根据小球所受的合力,结合牛顿第二定律求出小球的加速度.根据平行四边形定则求出小球的竖直位移,结合动能定理求出小球运动到A板的速度.
解答 解:(1)小球所受的合力${F}_{合}=\sqrt{(\frac{qU}{d})^{2}+(mg)^{2}}$,
根据牛顿第二定律得,小球的加速度a=$\frac{{F}_{合}}{m}=\frac{\sqrt{(\frac{qU}{d})^{2}+(mg)^{2}}}{m}$.
(2)小球运动的竖直位移为h,则有:$\frac{d}{h}=\frac{q\frac{U}{d}}{mg}$,解得h=$\frac{mgd}{q\frac{U}{d}}=\frac{mg{d}^{2}}{qU}$,
根据动能定理得,$qU+mgh=\frac{1}{2}m{v}^{2}$,
解得v=$\sqrt{\frac{2m{g}^{2}{d}^{2}}{qU}+\frac{2qU}{m}}$.
答:(1)小球加速度为$\frac{\sqrt{(\frac{qU}{d})^{2}+(mg)^{2}}}{m}$;
(2)运动A板时的速度为$\sqrt{\frac{2m{g}^{2}{d}^{2}}{qU}+\frac{2qU}{m}}$.
点评 本题考查带电小球在复合场中的运动,注意不能忽略小球的重力,对于第二问,也可以采用动力学知识进行求解.

练习册系列答案
相关题目
4.物理学的发展创新了很多研究问题的方法,如控制变量法、微元法等.下列叙述正确的是( )
| A. | 在探究物体的加速度与合力、加速度与质量的关系时,用到了等效替代的方法 | |
| B. | 在研究物体运动时,把物体看作质点,用到了微元法 | |
| C. | 合力和交变电流的有效值等概念的建立都体现了等效替代的思想 | |
| D. | 用比值法定义的物理量在物理学中占有相当大的比例,例如电场强度大小E=$\frac{F}{q}$、电容C=$\frac{Q}{U}$及加速度 a=$\frac{F}{m}$都是采用比值法定义的 |
19. 如图所示,光滑圆管固定在竖直平面内,有一小球在管内做圆周运动,忽略空气阻力,小球在运动过程中( )
如图所示,光滑圆管固定在竖直平面内,有一小球在管内做圆周运动,忽略空气阻力,小球在运动过程中( )
 如图所示,光滑圆管固定在竖直平面内,有一小球在管内做圆周运动,忽略空气阻力,小球在运动过程中( )
如图所示,光滑圆管固定在竖直平面内,有一小球在管内做圆周运动,忽略空气阻力,小球在运动过程中( )| A. | 动能不断变化 | B. | 机械能不守恒 | ||
| C. | 重力势能不断变化 | D. | 只有重力对小球做功 |
3.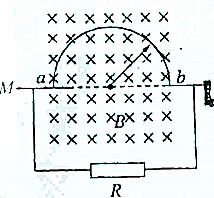 将硬导线中间一段折为半圆形是,使其半径为r(m),让它在磁感应强度为B(T)、方向如图所示的匀强磁场中绕轴MN匀速转动,转速为n(r/s),导线在a、b两处通过电刷与外电路连接,外电路接有阻值为R(Ω)的电阻,其余部分的电阻不计,则( )
将硬导线中间一段折为半圆形是,使其半径为r(m),让它在磁感应强度为B(T)、方向如图所示的匀强磁场中绕轴MN匀速转动,转速为n(r/s),导线在a、b两处通过电刷与外电路连接,外电路接有阻值为R(Ω)的电阻,其余部分的电阻不计,则( )
 将硬导线中间一段折为半圆形是,使其半径为r(m),让它在磁感应强度为B(T)、方向如图所示的匀强磁场中绕轴MN匀速转动,转速为n(r/s),导线在a、b两处通过电刷与外电路连接,外电路接有阻值为R(Ω)的电阻,其余部分的电阻不计,则( )
将硬导线中间一段折为半圆形是,使其半径为r(m),让它在磁感应强度为B(T)、方向如图所示的匀强磁场中绕轴MN匀速转动,转速为n(r/s),导线在a、b两处通过电刷与外电路连接,外电路接有阻值为R(Ω)的电阻,其余部分的电阻不计,则( )| A. | 通过电阻R的电流恒为$\frac{Bn{π}^{2}{r}^{2}}{R}$ | |
| B. | 电阻R两端的电压的最大值为Bnπ2r2 | |
| C. | 半圆导线从图示位置转过180°的过程中,通过电阻R的电荷量为$\frac{Bπ{r}^{2}}{R}$ | |
| D. | 电阻R上消耗的电功率为$\frac{(Bb{π}^{2}{r}^{2})^{2}}{2R}$ |
1. 带有活塞的汽缸内封闭一定量的理想气体.气体开始处于状态a;然后经过过程ab到达状态b或经过过程ac到状态c,b、c状态温度相同,如V-T图所示.设气体在状态b和状态c的压强分别为Pb和Pc,在过程ab和ac中吸收的热量分别为Qab和Qac,则( )
带有活塞的汽缸内封闭一定量的理想气体.气体开始处于状态a;然后经过过程ab到达状态b或经过过程ac到状态c,b、c状态温度相同,如V-T图所示.设气体在状态b和状态c的压强分别为Pb和Pc,在过程ab和ac中吸收的热量分别为Qab和Qac,则( )
 带有活塞的汽缸内封闭一定量的理想气体.气体开始处于状态a;然后经过过程ab到达状态b或经过过程ac到状态c,b、c状态温度相同,如V-T图所示.设气体在状态b和状态c的压强分别为Pb和Pc,在过程ab和ac中吸收的热量分别为Qab和Qac,则( )
带有活塞的汽缸内封闭一定量的理想气体.气体开始处于状态a;然后经过过程ab到达状态b或经过过程ac到状态c,b、c状态温度相同,如V-T图所示.设气体在状态b和状态c的压强分别为Pb和Pc,在过程ab和ac中吸收的热量分别为Qab和Qac,则( )| A. | pb>pc,Qab>Qac | B. | pb>pc,Qab<Qac | C. | pb<pc,Qab<Qac | D. | pb<pc,Qab>Qac |
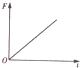
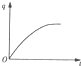
 如图甲所示,光滑金属导轨MN、PQ所在平面与水平面成θ角,M、P两端接一电阻R,整个装置处于方向垂直导轨平面上的匀强磁场中.t=0时对金属棒施加一平行于导轨的外力F,使金属棒ab由静止开始沿导轨向上运动,导轨电阻忽略不计.已知通过电阻R的感应电流I随时间t变化的关系如图乙所示.下列关于棒运动速度v、外力F、流过R的电量q以及闭合回路中磁通量的变化率$\frac{△φ}{△t}$随时间变化的图象正确的是( )
如图甲所示,光滑金属导轨MN、PQ所在平面与水平面成θ角,M、P两端接一电阻R,整个装置处于方向垂直导轨平面上的匀强磁场中.t=0时对金属棒施加一平行于导轨的外力F,使金属棒ab由静止开始沿导轨向上运动,导轨电阻忽略不计.已知通过电阻R的感应电流I随时间t变化的关系如图乙所示.下列关于棒运动速度v、外力F、流过R的电量q以及闭合回路中磁通量的变化率$\frac{△φ}{△t}$随时间变化的图象正确的是( )

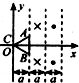 如图所示,两个垂直于纸面的匀强磁场方向相反,磁感应强度的大小均为B,磁场区域的宽度均为a.高度为a的正三角形导线框ABC从图示位置沿x轴正方向匀速穿过两磁场区域,以逆时针方向为电流的正方向.在下图中能正确描述感应电流I与线框移动距离x关系的是( )
如图所示,两个垂直于纸面的匀强磁场方向相反,磁感应强度的大小均为B,磁场区域的宽度均为a.高度为a的正三角形导线框ABC从图示位置沿x轴正方向匀速穿过两磁场区域,以逆时针方向为电流的正方向.在下图中能正确描述感应电流I与线框移动距离x关系的是( )



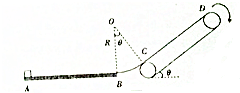 如图所示,光滑圆弧BC与水平面和传送带分别相切于B,C两点,圆弧所对应的圆心角θ=37°,圆弧BC的半径R=7m,足够长的传送带以恒定速率v=4m/s顺时针转动,传送带CD与水平面的夹角也为θ,一质量m=1kg的小滑块从A点以大小v0=10m/s的初速度向B点运动,A,B间的距离s=3.6m,已知小滑块与水平面、传送带之间的动摩擦因数均为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,光滑圆弧BC与水平面和传送带分别相切于B,C两点,圆弧所对应的圆心角θ=37°,圆弧BC的半径R=7m,足够长的传送带以恒定速率v=4m/s顺时针转动,传送带CD与水平面的夹角也为θ,一质量m=1kg的小滑块从A点以大小v0=10m/s的初速度向B点运动,A,B间的距离s=3.6m,已知小滑块与水平面、传送带之间的动摩擦因数均为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求: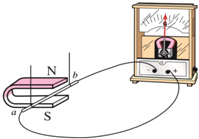 如图所示,是探究“什么情况下磁可以生电”的实验装置:
如图所示,是探究“什么情况下磁可以生电”的实验装置: