题目内容
10.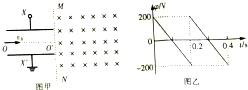 示波管中有两个偏转电极,其中一个电极XX′上可以接入仪器自身产生的锯齿形电压,叫扫描电压.如图甲所示,已知XX′极板长L=0.2$\sqrt{3}$m,板间距d=0.2m,在金属板右端竖直边界MN的右侧有一区域足够大的匀强磁场B=5×10-3T,方向垂直纸面向里.现将X′极板接地,X极板上电势φ随时间变化规律如图乙所示.有带正电的粒子流以速度v0=1×105m/s,沿水平中线OO′连续射入电场中,粒子的比荷$\frac{q}{m}$=1×108C/kg,重力忽略不计,在每个粒子通过电场的极短时间内,电场可视为匀强电场.(设两板外无电场,结果可用根式表示)求:
示波管中有两个偏转电极,其中一个电极XX′上可以接入仪器自身产生的锯齿形电压,叫扫描电压.如图甲所示,已知XX′极板长L=0.2$\sqrt{3}$m,板间距d=0.2m,在金属板右端竖直边界MN的右侧有一区域足够大的匀强磁场B=5×10-3T,方向垂直纸面向里.现将X′极板接地,X极板上电势φ随时间变化规律如图乙所示.有带正电的粒子流以速度v0=1×105m/s,沿水平中线OO′连续射入电场中,粒子的比荷$\frac{q}{m}$=1×108C/kg,重力忽略不计,在每个粒子通过电场的极短时间内,电场可视为匀强电场.(设两板外无电场,结果可用根式表示)求:(1)带电粒子射出电场时的最大速度;
(2)粒子在磁场中运动的最长时间和最短时间之比;
(3)从O′点射入磁场和距O′点下方$\frac{d}{4}$=0.05m处射入磁场的两个粒子,在MN上射出磁场时的出射点之间的距离.
分析 (1)粒子在电场中做类平抛运动,应用类平抛运动规律与动能定理可以求出带电粒子射出电场时的最大速率;
(2)粒子在磁场中做匀速圆周运动,应用牛顿第二定律求出粒子轨道半径,结合带电粒子在电场中向上偏转的情况与向下偏转的情况,画出运动的轨迹,由几何关系以及:$\frac{t}{T}=\frac{θ}{2π}$即可得出时间关系;
(3)分别从O′点和距O′点下方$\frac{d}{4}$=0.05m处射入磁场的两个粒子,由带电粒子在电场中运动的特点,求出粒子的偏转角,然后画出运动的轨迹,由几何关系即可得出结果.
解答 解:(1)带电粒子在偏转电场中做类平抛运动:
水平:$t=\frac{L}{v_0}=2\sqrt{3}×{10^{-6}}$s
竖直:$y=\frac{1}{2}a{t^2}=\frac{d}{2}$,其中$a=\frac{{q{U_1}}}{dm}$,
所以${U_1}=\frac{adm}{q}=\frac{100}{3}$V
当U>$\frac{100}{3}$V时进入电场中的粒子将打到极板上,即在电压等于$\frac{100}{3}$V时刻进入的粒子具有最大速度,所以由动能定理得:
$q\frac{U_1}{2}=\frac{1}{2}mv_t^2-\frac{1}{2}mv_0^2$,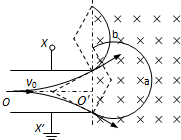 得:vt=$\frac{{2\sqrt{3}}}{3}×{10^5}$m/s,方向与水平成30°;
得:vt=$\frac{{2\sqrt{3}}}{3}×{10^5}$m/s,方向与水平成30°;
(2)计算可得,粒子射入磁场时的速度与水平方向的夹角为30°,从下极板边缘射出的粒子轨迹如图中a所示,磁场中轨迹所对的圆心角为240°,时间最长
从上极板边缘射出的粒子轨迹如图中b所示,磁场中轨迹所对应的圆心角为120°,时间最短
因为两粒子的周期$T=\frac{2πm}{Bq}$相同,所以粒子在磁场中运动的最长时间和最短时间之比为2:1
(3)如下图,从O′点射入磁场的粒子速度为v0,它在磁场中的出射点与入射点间距为d1=2R1
得:${R_1}=\frac{{m{v_1}}}{Bq}$,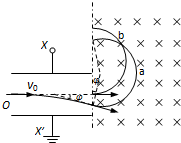 所以:${d_1}=\frac{{2m{v_0}}}{Bq}$
所以:${d_1}=\frac{{2m{v_0}}}{Bq}$
从距O′点下方$\frac{d}{4}$=0.05m处射入磁场的粒子速度与水平方向夹角φ,则它的速度为${v_2}=\frac{v_0}{cosϕ}$,它在磁场中的出射点与入射点间距为d2=2R2cosϕ,
由于${R_2}=\frac{{m{v_2}}}{Bq}$,所以${d_2}=\frac{{2m{v_0}}}{Bq}$
所以两个粒子向上偏移的距离相等!
所以:两粒子射出磁场的出射点间距仍为进入磁场时的间距,即$\frac{d}{4}=0.05$m
答:(1)带电粒子射出电场时的最大速率是$\frac{{2\sqrt{3}}}{3}×{10^5}$m/s,方向与水平成30°;
(2)粒子在磁场中运动的最长时间和最短时间之比是2:1;
(3)分别从O′点和距O′点下方$\frac{d}{4}$=0.05m处射入磁场的两个粒子,在MN上射出磁场时两出射点之间的距离是0.05m.
点评 本题以带电粒子在场中运动问题为命题背景考查学生的推理、分析和应用数学处理物理问题的能力.分析清楚粒子运动过程是正确解题的前提与关键,应用动能定理、类平抛运动规律、牛顿第二定律即可正确解题.

 一束由a、b两单色光组成的复色光以入射角θ由空气射到半圆形玻璃砖表面的A处,AB是半圆的直径.a、b两单色光组成的复色光进入玻璃后分为两束,分别为AC、AD.下列叙述正确的是( )
一束由a、b两单色光组成的复色光以入射角θ由空气射到半圆形玻璃砖表面的A处,AB是半圆的直径.a、b两单色光组成的复色光进入玻璃后分为两束,分别为AC、AD.下列叙述正确的是( )| A. | a光波的频率大于b光波的频率 | |
| B. | 它们从A到C和从A到D的时间分别为t1和t2,则t1=t2 | |
| C. | 将a、b两单色光光源分别放在水中同一点,水面上被照亮的区域,a光照亮的区域较大 | |
| D. | 用同一双缝干涉装置看到的a光干涉条纹间距比b光干涉条纹间距宽 |
 如图所示,固定的U型粗糙金属框架与水平面成θ角,将金属棒ab放在框架上,处于平衡状态,整个装置处于垂直框架平面的磁场中,现增加磁场的磁感应强度,在磁感应强度变化的瞬间( )
如图所示,固定的U型粗糙金属框架与水平面成θ角,将金属棒ab放在框架上,处于平衡状态,整个装置处于垂直框架平面的磁场中,现增加磁场的磁感应强度,在磁感应强度变化的瞬间( )| A. | ab中产生由b到a的感应电流 | B. | ab中产生由a到b的感应电流 | ||
| C. | ab受到水平框架平面向上的安培力 | D. | ab受到平行于水平面的安培力 |
 如图所示,竖直放置的上下固定的两气缸A、B之间用质量不计的活塞和轻杆连接,活塞与气缸壁之间无摩擦且不漏气,A的横截面积大于B的横截面积,A、B中气体的初始温度相同.现使A、B升高相同温度到再次达到稳定时,与初态相比A、B中气体的体积变化量为△VA、△VB,压强变化量为△PA、△PB,对活塞压力的变化量为△FA、△FB,则( )
如图所示,竖直放置的上下固定的两气缸A、B之间用质量不计的活塞和轻杆连接,活塞与气缸壁之间无摩擦且不漏气,A的横截面积大于B的横截面积,A、B中气体的初始温度相同.现使A、B升高相同温度到再次达到稳定时,与初态相比A、B中气体的体积变化量为△VA、△VB,压强变化量为△PA、△PB,对活塞压力的变化量为△FA、△FB,则( )| A. | 活塞和轻杆向上移动了一段距离 | B. | △FA>△FB | ||
| C. | △PA=△PB | D. | △VA=△VB |
 如图所示,ABCD为同种材料构成的柱形透明体的横截面,其中ABD部分为等腰直角三角形,BCD部分为半圆形.平行单色光从真空垂直射向AB面或AD面,折射率n=1.5,下列说法中正确的是( )
如图所示,ABCD为同种材料构成的柱形透明体的横截面,其中ABD部分为等腰直角三角形,BCD部分为半圆形.平行单色光从真空垂直射向AB面或AD面,折射率n=1.5,下列说法中正确的是( )| A. | 从AB射入的光线经一次全反射和一次折射后都能从BCD射出 | |
| B. | 从AB中点射入的光线恰好能从圆弧的中点射出 | |
| C. | 从AD射入的光线一定能从AD边垂直射出 | |
| D. | 从AD射入的光线一定能从BCD射出 |
 如图所示,光滑圆管固定在竖直平面内,有一小球在管内做圆周运动,忽略空气阻力,小球在运动过程中( )
如图所示,光滑圆管固定在竖直平面内,有一小球在管内做圆周运动,忽略空气阻力,小球在运动过程中( )| A. | 动能不断变化 | B. | 机械能不守恒 | ||
| C. | 重力势能不断变化 | D. | 只有重力对小球做功 |
| A. | 16个中子,8个质子 | B. | 8个中子,16个质子 | ||
| C. | 24个中子,8个质子 | D. | 8个中子,24个质子 |
 如图甲所示,光滑金属导轨MN、PQ所在平面与水平面成θ角,M、P两端接一电阻R,整个装置处于方向垂直导轨平面上的匀强磁场中.t=0时对金属棒施加一平行于导轨的外力F,使金属棒ab由静止开始沿导轨向上运动,导轨电阻忽略不计.已知通过电阻R的感应电流I随时间t变化的关系如图乙所示.下列关于棒运动速度v、外力F、流过R的电量q以及闭合回路中磁通量的变化率$\frac{△φ}{△t}$随时间变化的图象正确的是( )
如图甲所示,光滑金属导轨MN、PQ所在平面与水平面成θ角,M、P两端接一电阻R,整个装置处于方向垂直导轨平面上的匀强磁场中.t=0时对金属棒施加一平行于导轨的外力F,使金属棒ab由静止开始沿导轨向上运动,导轨电阻忽略不计.已知通过电阻R的感应电流I随时间t变化的关系如图乙所示.下列关于棒运动速度v、外力F、流过R的电量q以及闭合回路中磁通量的变化率$\frac{△φ}{△t}$随时间变化的图象正确的是( )

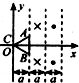 如图所示,两个垂直于纸面的匀强磁场方向相反,磁感应强度的大小均为B,磁场区域的宽度均为a.高度为a的正三角形导线框ABC从图示位置沿x轴正方向匀速穿过两磁场区域,以逆时针方向为电流的正方向.在下图中能正确描述感应电流I与线框移动距离x关系的是( )
如图所示,两个垂直于纸面的匀强磁场方向相反,磁感应强度的大小均为B,磁场区域的宽度均为a.高度为a的正三角形导线框ABC从图示位置沿x轴正方向匀速穿过两磁场区域,以逆时针方向为电流的正方向.在下图中能正确描述感应电流I与线框移动距离x关系的是( )


