题目内容
（13分）如图所示，在倾角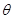
=370的固定斜面底端，放着一个质量为1Kg的物体，现对物体施加平行于斜面向上的恒力F＝20N，作用时间
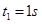时撤去拉力F，若物体与斜面间的动摩擦因数为μ=0.5，斜面足够长，取
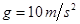，sin370=0.6,cos370=0.8。试求：
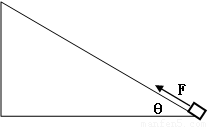
（1）撤去F时，物体的速度是多少？此过程中F做的功是多少？
（2）物体再返回到斜面低端时的速度是多少？
【答案】
(1)10m/s， 100J
（2）
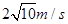
【解析】
试题分析：(1)撤去F前，物体受力如图示
由牛顿第二定律得：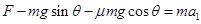
①
得： a1=10m/s2
由运动学公式：v1= a1t1 ②
得： v1=10m/s
这个过程的位移为: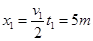
③
力F做的功为：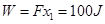
④
（2）撤去F后，物体受力如图示
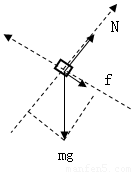
由牛顿第二定律：
⑤
得： a2= -10m/s2
依运动学公式：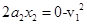
⑥
得：x2=5m
返回到斜面底端过程中，受力如图
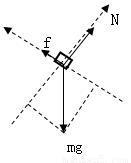
由牛顿第二定律得：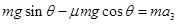
⑦
得： a3=2m/s2
依运动学公式：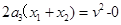
⑧
得：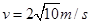 
考点：本题考查了受力分析和牛顿第二定律的应用
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
如图所示，在倾角为θ的光滑固定斜面上，劲度系数分别为k1、k2的两个轻弹簧平行于斜面悬挂着，k1在上 k2在下，两弹簧之间有一质量为m1的重物，现用力F（未知）沿斜面向上缓慢推动m2，当两弹簧的总长等于两弹簧的原长之和时，
（2009?深圳一模）如图所示，在倾角为30°的光滑斜面上固定一光滑金属导轨CDEFG，图中OH∥CD∥FG，∠DEF=60°，CD=DE=EF=FG=OE=L；一根质量为m、长度为2L的导体棒AB在电机牵引下，以恒定速度v0沿OH方向从斜面底端滑上导轨并到达斜面顶端，O是AB棒的中点，AB⊥OH．金属导轨的CD、FG段电阻不计，DEF段与AB棒材料与横截面积均相同，单位长度的电阻均为r，整个斜面处在垂直斜面向上、磁感应强度为B的匀强磁场中．求：
如图所示，在倾角为θ的绝缘斜面上，有相距为L的A、B两点，分别固定着两个带电量均为Q的正点电荷．O为AB连线的中点，a、b是AB连线上两点，其中Aa=Bb=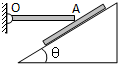
如图所示，在倾角θ 为37°的固定光滑斜面上放着一块质量不计的薄板，水平放置的棒OA，A端搁在薄板上，O端装有水平转轴，将薄板沿斜面向上和向下匀速拉动时所需拉力大小之比为3：4，则棒对板的压力大小之比为