题目内容
 (2009?深圳一模)如图所示,在倾角为30°的光滑斜面上固定一光滑金属导轨CDEFG,图中OH∥CD∥FG,∠DEF=60°,CD=DE=EF=FG=OE=L;一根质量为m、长度为2L的导体棒AB在电机牵引下,以恒定速度v0沿OH方向从斜面底端滑上导轨并到达斜面顶端,O是AB棒的中点,AB⊥OH.金属导轨的CD、FG段电阻不计,DEF段与AB棒材料与横截面积均相同,单位长度的电阻均为r,整个斜面处在垂直斜面向上、磁感应强度为B的匀强磁场中.求:
(2009?深圳一模)如图所示,在倾角为30°的光滑斜面上固定一光滑金属导轨CDEFG,图中OH∥CD∥FG,∠DEF=60°,CD=DE=EF=FG=OE=L;一根质量为m、长度为2L的导体棒AB在电机牵引下,以恒定速度v0沿OH方向从斜面底端滑上导轨并到达斜面顶端,O是AB棒的中点,AB⊥OH.金属导轨的CD、FG段电阻不计,DEF段与AB棒材料与横截面积均相同,单位长度的电阻均为r,整个斜面处在垂直斜面向上、磁感应强度为B的匀强磁场中.求:(1)导体棒在导轨DEF上滑动时电路中电流的大小;
(2)导体棒运动到DF位置时AB两端的电压;
(3)将导体棒从底端拉到斜面顶端过程电机对杆做的功.
分析:(1)根据感应电动势公式得出电动势与有效长度的关系,由题意得到电阻与有效长度的关系,根据欧姆定律得到导体棒在导轨DEF上滑动时电路中电流的大小;
(2)AB两端的电压等于AD、DF、FB三段感应电动势之和.AD、FB两段电压等于感应电动势.DF段根据电压分配求出.
(3)根据功能关系可知,导体棒从底端拉到斜面顶端过程电机对杆做的功等于导体棒增加的重力势能与电路产生的热量之和.AB棒在DEF上滑动时产生的电热Q1,数值上等于克服安培力做的功.
(2)AB两端的电压等于AD、DF、FB三段感应电动势之和.AD、FB两段电压等于感应电动势.DF段根据电压分配求出.
(3)根据功能关系可知,导体棒从底端拉到斜面顶端过程电机对杆做的功等于导体棒增加的重力势能与电路产生的热量之和.AB棒在DEF上滑动时产生的电热Q1,数值上等于克服安培力做的功.
解答: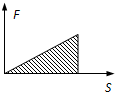 解:(1)设AB棒等效切割长度为l,则
解:(1)设AB棒等效切割长度为l,则
感应电动势为E=Blv0
回路电阻为R=3lr
回路电流为I=
=
(2)AB棒滑到DF处时
AB两端的电压UBA=UDA+UFD+UBF
UDA+UBF=BLv0
而UDF=
BLv0=
BLv0
得UBA=UDA+UFD+UBF=
BLv0
(3)导体棒重力势能的增加量△EP=mg(2L+Lcos30°)sin30°=
mgL
AB棒在DEF上滑动时产生的电热Q1,数值上等于克服安培力做的功Q1=W安
又因为F安∝S,如图,故 Q1=W安=
?
L=
AB棒在CDFG导轨上滑动时产生的电热Q2,电流恒定,电阻不变
则Q2=I2Rt=(
)2?3Lr?
=
得,电机做的功W=△EP+Q1+Q2=
(mgL+
)
答:(1)导体棒在导轨DEF上滑动时电路中电流的大小为流为
;
(2)导体棒运动到DF位置时AB两端的电压为
BLv0;
(3)将导体棒从底端拉到斜面顶端过程电机对杆做的功是
(mgL+
).
 解:(1)设AB棒等效切割长度为l,则
解:(1)设AB棒等效切割长度为l,则感应电动势为E=Blv0
回路电阻为R=3lr
回路电流为I=
| E |
| R |
| Bv0 |
| 3r |
(2)AB棒滑到DF处时
AB两端的电压UBA=UDA+UFD+UBF
UDA+UBF=BLv0
而UDF=
| 2lr |
| 3lr |
| 2 |
| 3 |
得UBA=UDA+UFD+UBF=
| 5 |
| 3 |
(3)导体棒重力势能的增加量△EP=mg(2L+Lcos30°)sin30°=
4+
| ||
| 4 |
AB棒在DEF上滑动时产生的电热Q1,数值上等于克服安培力做的功Q1=W安
又因为F安∝S,如图,故 Q1=W安=
| 0+F安max |
| 2 |
| ||
| 2 |
| ||
| 12r |
AB棒在CDFG导轨上滑动时产生的电热Q2,电流恒定,电阻不变
则Q2=I2Rt=(
| Bv0 |
| 3r |
| L |
| v0 |
| B2L2v0 |
| 3r |
得,电机做的功W=△EP+Q1+Q2=
4+
| ||
| 4 |
| B2L2v0 |
| 3r |
答:(1)导体棒在导轨DEF上滑动时电路中电流的大小为流为
| Bv0 |
| 3r |
(2)导体棒运动到DF位置时AB两端的电压为
| 5 |
| 3 |
(3)将导体棒从底端拉到斜面顶端过程电机对杆做的功是
4+
| ||
| 4 |
| B2L2v0 |
| 3r |
点评:本题难点在于求AB棒在DEF上滑动时产生的电热,根据导体棒克服安培力做功求解.容易出现的错误有两处:一是求AB的电压只考虑DF段电压.二是AB棒在DEF上滑动的距离当作Lsin30°.

练习册系列答案
相关题目
 (2009?深圳一模)在光滑水平面上有两个小木块A和B,其质量mA=1kg、mB=4kg,它们中间用一根轻质弹簧相连.一颗水平飞行的子弹质量为m=50g,以V0=500m/s的速度在极短时间内射穿两木块,已知射穿A木块后子弹的速度变为原来的
(2009?深圳一模)在光滑水平面上有两个小木块A和B,其质量mA=1kg、mB=4kg,它们中间用一根轻质弹簧相连.一颗水平飞行的子弹质量为m=50g,以V0=500m/s的速度在极短时间内射穿两木块,已知射穿A木块后子弹的速度变为原来的 (2009?深圳一模)如图所示,匀强磁场的方向竖直向下.磁场中有光滑的水平桌面,在桌面上平放着内壁光滑、底部有带电小球的试管.试管在水平拉力F作用下向右匀速运动,带电小球能从管口处飞出.关于带电小球及其在离开试管前的运动,下列说法中正确的是( )
(2009?深圳一模)如图所示,匀强磁场的方向竖直向下.磁场中有光滑的水平桌面,在桌面上平放着内壁光滑、底部有带电小球的试管.试管在水平拉力F作用下向右匀速运动,带电小球能从管口处飞出.关于带电小球及其在离开试管前的运动,下列说法中正确的是( )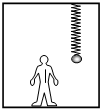 (2009?深圳一模)如图所示,轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小铁球,在电梯运行时,乘客发现弹簧的伸长量比电梯静止时的伸长量小,这一现象表明此过程中( )
(2009?深圳一模)如图所示,轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小铁球,在电梯运行时,乘客发现弹簧的伸长量比电梯静止时的伸长量小,这一现象表明此过程中( ) (2009?深圳一模)一根长为l的线吊着一质量为m的带电量为q的小球静止在水平向右的匀强电场中,如图所示,线与竖直方向成37°角,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响,(重力加速度为g),求:
(2009?深圳一模)一根长为l的线吊着一质量为m的带电量为q的小球静止在水平向右的匀强电场中,如图所示,线与竖直方向成37°角,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响,(重力加速度为g),求: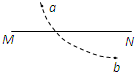 (2009?深圳一模)如图所示,MN是一负点电荷产生的电场中的一条电场线.一个带正电的粒子(不计重力)从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( )
(2009?深圳一模)如图所示,MN是一负点电荷产生的电场中的一条电场线.一个带正电的粒子(不计重力)从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( )