题目内容
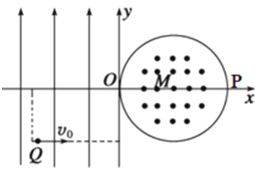
【题目】如图所示，在平面直角坐标系 xOy 内，第二、三象限内存在沿 y 轴正方向的匀强电场，第一、四象限内存在半径为 L 的圆形匀强磁场，磁场方向垂直于坐标平面向外。 一个比荷（荷质比）为 K 的带正电的粒子从第三象限中的 Q（-2L，-L）点以速度 v0 沿 x 轴正方向射出，恰好从坐标原点 O 进入磁场，从 P（2L，0）点射出磁场。不计粒子重力，求：
(1)电场强度 E；
(2)从P点射出时速度的大小；
(3)粒子在磁场与电场中运动时间。
【答案】(1)
；(2)
；(3)
【解析】
(1)带电粒子在匀强电场中做类平抛运动，
加速度：
a=
=EK
在电场中运动的时间：
t1=
沿y轴正方向，则有：
=L
即：
则：
E=
(2)带电粒子刚进入磁场时，沿y轴正方向的分速度：
vy=at1=EK·
则带电粒子进入磁场时的速度：
v=
由于在磁场中洛仑兹力不改变带电粒子速度大小，则：
vP=v=
(3)由图可知，设带电粒子进入磁场时速度v与x轴正方向夹角α，则满足：
tanα=
=1
得：
α=45°
则偏转圆的圆心角：
由几何关系可知，偏转半径：
R=
则粒子在磁场中运动时间：
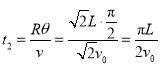
粒子在磁场与电场中运动时间：
练习册系列答案
相关题目
