题目内容
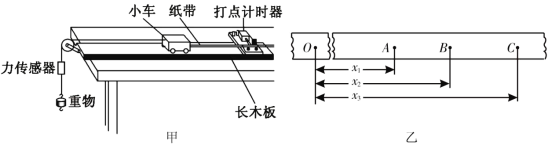
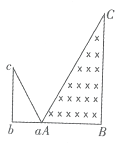
【题目】光滑水平面上放着两完全相同的小球A和B，其质量均为0.02kg，A靠在竖直墙壁上，一原长为12cm的轻质弹簧将A、B连在一起，压缩弹簧使其长度为4cm时，用销钉挡住B不动。拔掉销钉，当弹簧长度第2次达到（12+
）cm时，从A、B之间撤去弹簧，之后A、B发生弹性碰撞，分别冲向长为0.5m、倾角为53°的光滑斜面（机械能不损失），并落到足够长的水平固定平台上，已知弹簧弹性势能的表达式为Ep=
kx2，其中劲度系数k=200N/m，x为弹簧形变量；sin53°=0.8，cos53°=0.6，g=10m/s2．求：
（1）弹簧首次恢复到原长时B球的速度大小；
（2）从撤去弹簧到两球相碰经历的时间；
（3）两球在平台上第一次落点间的距离。
【答案】（1）8m/s；（2）
s；（3）1.536m。
【解析】
（1）至弹簧恢复原长时，由机械能守恒定律得：
kx12=
代入数据得vB=8m/s
（2）弹簧恢复原长后，A开始运动，至撤去弹簧
由动量守恒定律得mBvB=mAvA1+mBvB1
由能量守恒定律kx12
kx22=mAvA12+mBvB12
代入数据得vA1=5m/s
vB1=3m/s
从撤去弹簧到A、B相碰经历时间t=
解得t=s
（3）A、B弹性碰撞，机械能动量均守恒
速度交换vA2=3m/s；vB2=5m/s
到达斜面顶端的速度分别为vA3，vB3
其中斜面上运动的加速度a=8m/s2
得vA3=1m/s，vB3=
m/s
在平台上的水平位移x=v3cos53°
最终可得两球落点的水平距离d=1.536m
练习册系列答案
相关题目
