题目内容
(10分)如图所示,长木板A上右端有一物块B,它们一起在光滑的水平面上向左做匀速运动,速度v0=2m/s。木板左侧有一个与木板A等高的固定物体C。已知长木板A的质量为mA=1.0kg,物块B的质量为mB=3.0kg,物块B与木板A间的动摩擦因数μ=0.5,取g=10m/s2。
(1)若木板A足够长,A与C第一次碰撞后,A立即与C粘在一起,求物块 B在木板A上滑行的距离L应是多少;
(2)若木板足够长,A与C发生碰撞后弹回(碰撞时间极短,没有机械能损失),求第一次碰撞后A、B具有共同运动的速度v;
(3)若木板A长为0.48m,且A与C每次碰撞均无机械能损失,求A与C碰撞几次,B可脱离A?
(1)0.40m (2)1 m/s (3)第二次碰后B可脱离A板
解析试题分析:(1)A与C碰撞后速度即变为0,而B将继续运动,受摩擦力作用,速度由v0减到0,由动能定理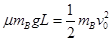
L=0.40m (2分)
(2)A与C发生弹性碰撞后,速度大小仍为v0,方向相反,以A、B为研究对象,设A、B有共同的速度v,水平方向不受外力作用,系统动量守恒,设向左为正
v= 1 m/s ,方向水平向左 (3分)
1 m/s ,方向水平向左 (3分)
(3)第一次A与C碰后,A、B有共同的速度v,B在A上相对于A滑行L1,则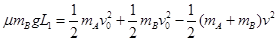
L1=0.40m (2分)
第二次A与C碰后至A、B有共同的速度 ,B在A上相对于A滑行L2,则
,B在A上相对于A滑行L2,则

由以上两式,可得L2=0.10m (2分)
则L1+ L2=0.5m>0.48m
即第二次碰后B可脱离A板 (1分)
考点:本题考查动量守恒、动能定理.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
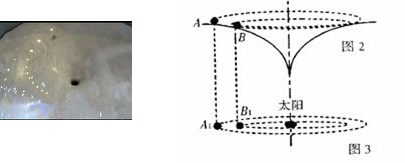
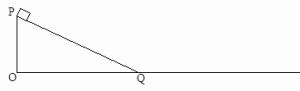
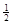 L,在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B,则:
L,在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B,则: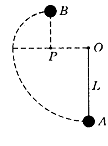
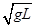 ,则在小球从A到B的过程中克服空气阻力做了多少功?
,则在小球从A到B的过程中克服空气阻力做了多少功?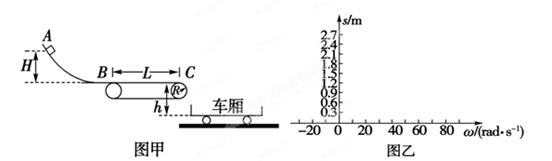
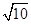 m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求
m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求 
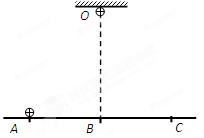
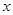 的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,然后沿半圆轨道运动到C处后,又正好落回到A点,求:
的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,然后沿半圆轨道运动到C处后,又正好落回到A点,求: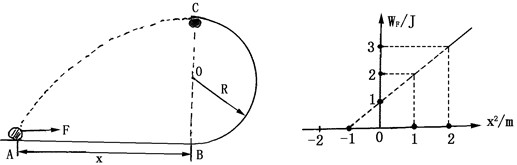
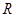 、
、 表示);
表示);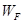 与
与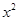 的关系如图所示,试求小球的质量和圆轨道半径。(
的关系如图所示,试求小球的质量和圆轨道半径。(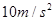 )
)