题目内容
13.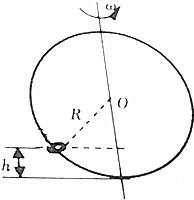 如图所示,半径为R的光滑大环上套有一个质量为m的小环,当大环以角速度ω绕着通过环心O的竖直轴旋转时,要使小环随大环在一定高度h(h>0)处做水平匀速圆周运动.则角速度ω的取值应满足( )
如图所示,半径为R的光滑大环上套有一个质量为m的小环,当大环以角速度ω绕着通过环心O的竖直轴旋转时,要使小环随大环在一定高度h(h>0)处做水平匀速圆周运动.则角速度ω的取值应满足( )| A. | ω>0 | B. | ω>$\sqrt{\frac{g}{R}}$ | C. | ω<$\sqrt{\frac{g}{R}}$ | D. | ω=$\sqrt{\frac{g}{R}}$ |
分析 小环绕着环心的竖直轴旋转时做匀速圆周运动,由其重力和圆环的支持力的合力提供向心力,根据向心力公式及几何关系即可求解.
解答 解:设半径方向与水平方向的夹角为θ,
根据合外力提供向心力得:
$\frac{mg}{tanθ}={mω}^{2}r$=mω2Rcosθ
解得:ω=$\sqrt{\frac{g}{Rsinθ}}=\sqrt{\frac{g}{R-h}}$>$\sqrt{\frac{g}{R}}$
故选:B
点评 本题主要考查了向心力公式的直接应用,能熟练运用几何关系进行求解,难度不大,属于基础题.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
5.某物体做初速度为零的匀加速直线运动,当其运动速度等于其末速度的$\frac{1}{3}$时.剩余的路程占其全程的( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{8}{9}$ |
8.下列陈述中正确的是( )
| A. | 泊松亮斑是泊松通过实验发现的,它属于光的衍射现象 | |
| B. | 激光是自然界中相干性很好的单色光 | |
| C. | 电磁波包括无线电波、伦琴射线等 | |
| D. | 光的偏振现象说明光是一种纵波 |
9.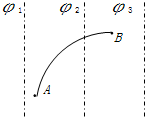 如图,三条虚线表示某电场的三个等势面,其中φ1=-30V,φ2=-20V,φ3=-10V,一带电粒子只受电场力作用,沿图中实线轨迹从A运动到B,则( )
如图,三条虚线表示某电场的三个等势面,其中φ1=-30V,φ2=-20V,φ3=-10V,一带电粒子只受电场力作用,沿图中实线轨迹从A运动到B,则( )
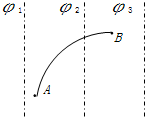 如图,三条虚线表示某电场的三个等势面,其中φ1=-30V,φ2=-20V,φ3=-10V,一带电粒子只受电场力作用,沿图中实线轨迹从A运动到B,则( )
如图,三条虚线表示某电场的三个等势面,其中φ1=-30V,φ2=-20V,φ3=-10V,一带电粒子只受电场力作用,沿图中实线轨迹从A运动到B,则( )| A. | 粒子带正电 | B. | 粒子的速度变大 | ||
| C. | 粒子的加速度变大 | D. | 粒子的电势能变大 |
 如图所示,L1标有“6V 3W”,L2标有“9V 3W”,开关S闭合之后,发现其中有一盏灯正常发光,而另一盏灯发光比较暗.求:
如图所示,L1标有“6V 3W”,L2标有“9V 3W”,开关S闭合之后,发现其中有一盏灯正常发光,而另一盏灯发光比较暗.求: 如图所示,一物体从O点开始做一初速为零、加速度为10m/s2的匀加速直线运动,通过长为1.2m的AB段历时0.2s,求OA段的长度.
如图所示,一物体从O点开始做一初速为零、加速度为10m/s2的匀加速直线运动,通过长为1.2m的AB段历时0.2s,求OA段的长度.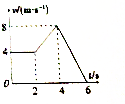 某质点做直线运动的v-t图象如图所示,通过图象回答下列问题:
某质点做直线运动的v-t图象如图所示,通过图象回答下列问题: