题目内容
质量为m的小球，用长为l的细线悬挂在O点，在O点的正下方| l |
| 2 |
分析：让小球从静止释放，当小球第一次经过最低点时，线速度不变，半径变大，根据v=rω，a=
判断角速度、向心加速度的变化，根据牛顿第二定律判断悬绳拉力的变化．
| v2 |
| r |
解答：解：小球通过最低点时，线速度不变，根据ω=
知，半径增大，则角速度减小．根据a=
知，半径增大，向心加速度减小．根据牛顿第二定律知，F-mg=m
，得F=mg+m
知拉力减小．故B正确，A、C、D错误．
故选B．
| v |
| r |
| v2 |
| r |
| v2 |
| r |
| v2 |
| r |
故选B．
点评：解决本题的关键抓住通过最低点的线速度不变，根据半径的变化判断角速度、向心加速度等变化．
练习册系列答案
相关题目
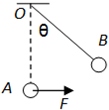一质量为m的小球，用长为L的轻绳悬挂在 O点，小球在水平恒力F作用下，从静止开始由平衡位置P点移动到Q点，此时绳与竖直方向的偏角为θ如图所示，则力F所做的功为（ ）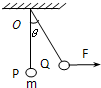
一质量为m的小球，用长为L不可伸长的轻绳悬挂于O点，小球在水平力F的作用下从平衡位置P点缓慢移动到Q点，如图所示，则此过程中力F做的功为（ ）
质量为m的小球，用长为l的细线悬挂在O点，在O点的正下方
一质量为m的小球，用长为L的轻绳悬挂于O点，小球在水平F作用下，从静止由最底位置P点拉到Q点，．如图所示，此时悬线与竖直方向夹角为θ，①当F为恒力时，拉力F做功为W1，②当F使小球缓慢上升时，拉力F做功为W2（ ）
一质量为 m 的小球，用长为L的轻绳悬挂于O点，在水平拉力F作用下，小球以恒定的速率在竖直平面内由A点运动到B点，下列说法正确的是（ ）| A、拉力的功率不断减小 | B、拉力逐渐增大 | C、物体所受的合外力为零 | D、拉力所做的功为FLsinθ |