题目内容
11. 如图所示,固定位置在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m(质量分布均匀)的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为u.现杆在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离L时,速度恰好达到最大(运动过程中杆始终与导轨保持垂直).设杆接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.则此过程( )
如图所示,固定位置在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m(质量分布均匀)的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为u.现杆在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离L时,速度恰好达到最大(运动过程中杆始终与导轨保持垂直).设杆接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.则此过程( )| A. | 杆的速度最大值为$\frac{(F-μmg)R}{{B}^{2}{d}^{2}}$ | |
| B. | 流过电阻R的电量为$\frac{Bdl}{R+r}$ | |
| C. | 恒力F做的功与摩擦力做的功之和等于杆动能的变化量 | |
| D. | 恒力F做的功与安倍力做的功之和大于杆动能的变化量 |
分析 A、当杆子所受的合力为零时速度最大,根据平衡结合闭合电路欧姆定律以及切割产生的感应电动势公式求出最大速度.
B、根据法拉第电磁感应定律求出平均感应电动势,从而得出平均感应电流,根据q=It求出通过电阻的电量.
CD、根据动能定理判断恒力、摩擦力、安培力做功与动能的关系.
解答 解:A、当杆的速度达到最大时,安培力F安=$\frac{{B}^{2}{d}^{2}v}{R+r}$,杆受力平衡,故F-μmg-F安=0,所以v=$\frac{(F-μmg)(R+r)}{{B}^{2}{d}^{2}}$.故A错误.
B、流过电阻R的电荷量为q=It=$\frac{△Φ}{R+r}$=$\frac{Bdl}{R+r}$,故B正确;
CD、根据动能定理,恒力F、安培力、摩擦力做功的代数和等于杆动能的变化量,由于摩擦力做负功,所以恒力F、安培力做功的代数和大于杆动能的变化量.故C错误、D正确.
故选:BD.
点评 本题综合运用了法拉第电磁感应定律的公式E=$N\frac{△Φ}{△t}$以及切割产生的感应电动势的大小公式E=BLv,知道两公式的区别.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
2.下列单位属于电容单位的是( )
| A. | F | B. | N | C. | C | D. | $\frac{V}{M}$ |
19. 构建和谐、节约型社会深得民心,这体现于生活的方方面面,自动充电式电动车就是很好的一例.在电动车的前轮处装有发电机,发电机与蓄电池连接.当骑车者用力蹬车或电动自行车自动滑行时,自行车就可以连通发电机对蓄电池充电,将其它形式的能转化成电能储存起来.某人骑车以500J的初动能在粗糙的水平面上滑行,第一次关闭自动充电装置让车自由滑行,其动能随位移变化的关系如图线①所示;第二次启动自动充电装置,其动能随位移变化的关系如图线②所示.设两种情况下自行车受到的阻力(包括空气阻力和摩擦阻力等)恒定不变,则下列说法中正确的是( )
构建和谐、节约型社会深得民心,这体现于生活的方方面面,自动充电式电动车就是很好的一例.在电动车的前轮处装有发电机,发电机与蓄电池连接.当骑车者用力蹬车或电动自行车自动滑行时,自行车就可以连通发电机对蓄电池充电,将其它形式的能转化成电能储存起来.某人骑车以500J的初动能在粗糙的水平面上滑行,第一次关闭自动充电装置让车自由滑行,其动能随位移变化的关系如图线①所示;第二次启动自动充电装置,其动能随位移变化的关系如图线②所示.设两种情况下自行车受到的阻力(包括空气阻力和摩擦阻力等)恒定不变,则下列说法中正确的是( )
 构建和谐、节约型社会深得民心,这体现于生活的方方面面,自动充电式电动车就是很好的一例.在电动车的前轮处装有发电机,发电机与蓄电池连接.当骑车者用力蹬车或电动自行车自动滑行时,自行车就可以连通发电机对蓄电池充电,将其它形式的能转化成电能储存起来.某人骑车以500J的初动能在粗糙的水平面上滑行,第一次关闭自动充电装置让车自由滑行,其动能随位移变化的关系如图线①所示;第二次启动自动充电装置,其动能随位移变化的关系如图线②所示.设两种情况下自行车受到的阻力(包括空气阻力和摩擦阻力等)恒定不变,则下列说法中正确的是( )
构建和谐、节约型社会深得民心,这体现于生活的方方面面,自动充电式电动车就是很好的一例.在电动车的前轮处装有发电机,发电机与蓄电池连接.当骑车者用力蹬车或电动自行车自动滑行时,自行车就可以连通发电机对蓄电池充电,将其它形式的能转化成电能储存起来.某人骑车以500J的初动能在粗糙的水平面上滑行,第一次关闭自动充电装置让车自由滑行,其动能随位移变化的关系如图线①所示;第二次启动自动充电装置,其动能随位移变化的关系如图线②所示.设两种情况下自行车受到的阻力(包括空气阻力和摩擦阻力等)恒定不变,则下列说法中正确的是( )| A. | 自行车受到的阻力为50N | B. | 自行车受到的阻力约为83N | ||
| C. | 第二次向蓄电池所充的电能是200J | D. | 第二次向蓄电池所充的电能是250J |
6. 如图所示为伽利略设计的世界上第一个温度计示意图,上部是一个球形容器,里面有一定质量的空气,下部是一根细管,细管插入带色液体中,制作时先给球形容器微微加热,跑出一些空气,插入液体中时,带色液体上升到管内某一高度.测量时球形容器与所测物质接触.已知外界大气压为p0,并保持不变,所测温度为t1时,管内液面在a位置,管内气体分子的平均动能为Ek1,气体压强为p1,管内气体内能为E1;所测温度为t2时,管内液面在b位置,其他三个量分别为Ek2、p2、E2,由此可知( )
如图所示为伽利略设计的世界上第一个温度计示意图,上部是一个球形容器,里面有一定质量的空气,下部是一根细管,细管插入带色液体中,制作时先给球形容器微微加热,跑出一些空气,插入液体中时,带色液体上升到管内某一高度.测量时球形容器与所测物质接触.已知外界大气压为p0,并保持不变,所测温度为t1时,管内液面在a位置,管内气体分子的平均动能为Ek1,气体压强为p1,管内气体内能为E1;所测温度为t2时,管内液面在b位置,其他三个量分别为Ek2、p2、E2,由此可知( )
 如图所示为伽利略设计的世界上第一个温度计示意图,上部是一个球形容器,里面有一定质量的空气,下部是一根细管,细管插入带色液体中,制作时先给球形容器微微加热,跑出一些空气,插入液体中时,带色液体上升到管内某一高度.测量时球形容器与所测物质接触.已知外界大气压为p0,并保持不变,所测温度为t1时,管内液面在a位置,管内气体分子的平均动能为Ek1,气体压强为p1,管内气体内能为E1;所测温度为t2时,管内液面在b位置,其他三个量分别为Ek2、p2、E2,由此可知( )
如图所示为伽利略设计的世界上第一个温度计示意图,上部是一个球形容器,里面有一定质量的空气,下部是一根细管,细管插入带色液体中,制作时先给球形容器微微加热,跑出一些空气,插入液体中时,带色液体上升到管内某一高度.测量时球形容器与所测物质接触.已知外界大气压为p0,并保持不变,所测温度为t1时,管内液面在a位置,管内气体分子的平均动能为Ek1,气体压强为p1,管内气体内能为E1;所测温度为t2时,管内液面在b位置,其他三个量分别为Ek2、p2、E2,由此可知( )| A. | t1<t2 | B. | p1<p2 | C. | Ek1<Ek2 | D. | E1>E2 |
3.(多选题)下列说法中正确的是( )
| A. | 位移是从起点到终点的有向线段 | |
| B. | 力和速度都是矢量,路程是标量 | |
| C. | 速度越大加速度就越大 | |
| D. | 物体竖直向下运动且只受重力,这就是自由落体运动 |
1. 三个质点A、B、C的运动轨迹如图所示,三个质点同时从N点出发,同时到达M点,设无往返运动,下列说法正确的是( )
三个质点A、B、C的运动轨迹如图所示,三个质点同时从N点出发,同时到达M点,设无往返运动,下列说法正确的是( )
 三个质点A、B、C的运动轨迹如图所示,三个质点同时从N点出发,同时到达M点,设无往返运动,下列说法正确的是( )
三个质点A、B、C的运动轨迹如图所示,三个质点同时从N点出发,同时到达M点,设无往返运动,下列说法正确的是( )| A. | 三个质点从N到M的平均速度相同 | |
| B. | 三个质点任意时刻的速度方向都相同 | |
| C. | 三个质点从N点出发到任意时刻的平均速度都相同 | |
| D. | 三个质点从Ν到Μ的平均速率相同 |


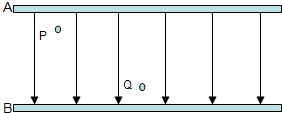 如图所示,平行的金属板A、B间是匀强电场.两板间的距离为5cm,两板间的电压为60V.P、Q为电场中的两个点,P点离A板0.5cm,Q点离B板0.5cm.
如图所示,平行的金属板A、B间是匀强电场.两板间的距离为5cm,两板间的电压为60V.P、Q为电场中的两个点,P点离A板0.5cm,Q点离B板0.5cm.