题目内容
16.如图1为验证牛顿第二定律的实验装置示意图.图中打点计时器的电源为50Hz的交流电源,打点的时间间隔用△t表示.在小车质量未知的情况下,某同学设计了一种方法用来研究“在外力一定的条件下,物体的加速度与其质量间的关系”.
(1)完成下列实验步骤中的填空:
①平衡小车所受的阻力:小吊盘中不放物块,调整木板 右端的高度,用手轻拨小车,直到打点计时器打出一系列间隔均匀的点.
②按住小车,在小吊盘中放入适当质量的物块,在小车中放入砝码.
③打开打点计时器电源,释放小车,获得带有点列的纸袋,在纸袋上标出小车中砝码的质量m.
④按住小车,改变小车中砝码的质量,重复步骤③.
⑤在每条纸带上清晰的部分,没5个间隔标注一个计数点.测量相邻计数点的间距s1,s2,….求出与不同m相对应的加速度a.
⑥以砝码的质量m为横坐标$\frac{1}{a}$为纵坐标,在坐标纸上做出$\frac{1}{a}$-m关系图线.若加速度与小车和砝码的总质量成反比,则$\frac{1}{a}$与m处应成线性关系(填“线性”或“非线性”).
(2)完成下列填空:
(ⅰ)本实验中,为了保证在改变小车中砝码的质量时,小车所受的拉力近似不变,小吊盘和盘中物块的质量之和应满足的条件是远小于小车的质量.
(ⅱ)设纸带上三个相邻计数点的间距为s1、s2、s3.a可用s1、s3和△t表示为a=$\frac{{s}_{3}-{s}_{1}}{2(△t)^{2}}$
图2为用米尺测量某一纸带上的s1、s3的情况,由图可读出s1=2.45cm,s3=4.70.
由此求得加速度的大小a=1.15m/s2.

(ⅲ)图3为所得实验图线的示意图.设图中直线的斜率为k,在纵轴上的截距为b,若牛顿定律成立,则小车受到的拉力为$\frac{1}{k}$,小车的质量为$\frac{b}{k}$.
分析 (1)根据实验注意事项分析答题;
(2)由图示刻度尺读出其示数;应用匀变速运动的推论求出加速度;
(3)由牛顿第二定律求出图象的函数表达式,然后根据图示图象分析答题.
解答 解:(1)①在平衡摩擦力时,应小吊盘中不放物块,调整木板右端的高度,用手轻拨小车,直到打点计时器打出一系列均匀的点,则此时说明小车做匀速运动;
⑥由牛顿第二定律可知,a=$\frac{F}{m}$;则说明加速度的倒数与m成线性关系;
(2)i探究牛顿第二定律实验时,当小吊盘和盘中物块的质量之和远小于小车和车中砝码的总质量时,可以近似认为小车受到的拉力等于小吊盘和盘中物块受到的重力,认为小车受到的拉力不变.
(ii)图示刻度尺可知,s1=3.70-1.25=2.45cm;s3=12.0-7.30=4.70cm;
由匀变速直线运动的推论:△x=at2可知,加速度:a=$\frac{{s}_{3}-{s}_{1}}{2(△t)^{2}}$=$\frac{4.70-2.45}{2×(0.1)^{2}}$×10-2=1.12m/s2;
(iii)设小车质量为M,由牛顿第二定律得:F=(M+m)a,则$\frac{1}{a}$=$\frac{1}{F}$m+$\frac{M}{F}$,
由图示图象可知:k=$\frac{1}{F}$,则拉力:F=$\frac{1}{k}$,b=$\frac{M}{F}$,则:M=bF=$\frac{b}{k}$;
故答案为:(1)①间隔均匀;⑥线性;
(2)i远小于小车的质量;
ii、$\frac{{s}_{3}-{s}_{1}}{2(△t)^{2}}$;2.45;4.70;1.15;
iii、$\frac{1}{k}$;$\frac{b}{k}$.
点评 本题考查了实验注意事项、刻度尺读数、求加速度、求拉力与小车质量问题,知道实验注意事项、实验原理、应用匀变速直线运动的推论、牛顿第二定律即可正确解题.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 如图所示,用两根同样长的细绳把两个带同种电荷的小球悬挂在同一点.两球的质量分别为mA、mB,A球和B球所带的电荷量分别为qA、qB.两球静止时,悬线与竖直线的偏角分别为α和β,则可能正确的是( )
如图所示,用两根同样长的细绳把两个带同种电荷的小球悬挂在同一点.两球的质量分别为mA、mB,A球和B球所带的电荷量分别为qA、qB.两球静止时,悬线与竖直线的偏角分别为α和β,则可能正确的是( )| A. | mA>mB,qA<qB,α>β | B. | mA<mB,qA<qB,α<β | C. | mA=mB,qA<qB,α<β | D. | mA=mB,qA>qB,α=β |
 如图所示,固定位置在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m(质量分布均匀)的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为u.现杆在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离L时,速度恰好达到最大(运动过程中杆始终与导轨保持垂直).设杆接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.则此过程( )
如图所示,固定位置在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m(质量分布均匀)的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为u.现杆在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离L时,速度恰好达到最大(运动过程中杆始终与导轨保持垂直).设杆接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.则此过程( )| A. | 杆的速度最大值为$\frac{(F-μmg)R}{{B}^{2}{d}^{2}}$ | |
| B. | 流过电阻R的电量为$\frac{Bdl}{R+r}$ | |
| C. | 恒力F做的功与摩擦力做的功之和等于杆动能的变化量 | |
| D. | 恒力F做的功与安倍力做的功之和大于杆动能的变化量 |
 如图所示,小球从A点以初速度V0沿粗糙斜面向上运动,到达最高点B后返回.C为AB的中点.下列说法中正确的是( )
如图所示,小球从A点以初速度V0沿粗糙斜面向上运动,到达最高点B后返回.C为AB的中点.下列说法中正确的是( )| A. | 小球从A出发到返回A的过程,位移为零,外力做功为零 | |
| B. | 小球从C到A过程与从B到C过程,减少的动能相等 | |
| C. | 小球从A到B过程与从B到A过程,损失的机械能相等 | |
| D. | 小球从A到C过程与从C烈B过程,速度的变化量相等 |
| A. | S | B. | 2 s | C. | $\frac{1}{2}$s | D. | 4 s |
| A. | 速度开始减小,直到加速度等于零为止 | |
| B. | 位移一直增加,直到加速度为零为止 | |
| C. | 速度一直增加,直到加速度等于零为止 | |
| D. | 位移始终增加 |
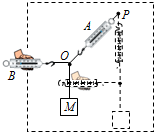 某同学用如图所示的实验装置验证“力的平行四边形定则”.将弹簧测力计A挂于固定点P,下端用细线挂一重物M.弹簧测力计B的挂钩处系一细线,把细线的另一端系在弹簧测力计A下端细线上的O点处,手持弹簧测力计B水平向左拉,使重物静止在如图所示的位置.若已知重物所受的重力为G,弹簧测力计A的拉力方向与竖直方向的夹角为θ,且两弹簧测力计的拉力均不超出它们的量程,则两弹簧测力计的拉力分别为FA=$\frac{G}{cosθ}$,FB=Gtanθ.
某同学用如图所示的实验装置验证“力的平行四边形定则”.将弹簧测力计A挂于固定点P,下端用细线挂一重物M.弹簧测力计B的挂钩处系一细线,把细线的另一端系在弹簧测力计A下端细线上的O点处,手持弹簧测力计B水平向左拉,使重物静止在如图所示的位置.若已知重物所受的重力为G,弹簧测力计A的拉力方向与竖直方向的夹角为θ,且两弹簧测力计的拉力均不超出它们的量程,则两弹簧测力计的拉力分别为FA=$\frac{G}{cosθ}$,FB=Gtanθ.