��Ŀ����
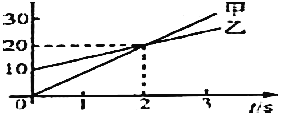
����Ŀ����ͼ����ʾ����ƽ�н����������ͼ����ʾ��ʱ��t�仯�ĵ�ѹU�������糡�ɿ������ȵģ����������糡���峤L=0.2m��������d=0.2m���ڽ������Ҳ���һ�߽�ΪMN�������㹻�����ǿ�ų���MN����������OO�䴹ֱ���Ÿ�Ӧǿ��B=5��10��3T������ֱֽ��������д����������������������OO����������糡�У���֪ÿ�������ٶ�v0=105 m/s���Ⱥ�q/m=108 C/kg���������Բ��ƣ���ÿ������ͨ���糡����ļ���ʱ���ڣ��糡�������Ǻ㶨����ģ�
��1�����������������糡ʱ������ٶȣ�
��2��֤����������ʱ�̴ӵ糡����Ĵ������ӣ�����ų�ʱ��MN�ϵ���������MN�ϳ����ľ���Ϊ��ֵ��д���þ���ı���ʽ��
��3���ӵ糡����Ĵ������ӣ�����ų��˶�һ��ʱ���������ų����������ڴų����˶����ʱ������ʱ�䣮
���𰸡�
��1���⣺ƫת��ѹ��0��200V�ı仯�У����������ܶ�������糡��Ҳ����ֻ�в�������������糡��
��ƫת�ĵ�ѹΪU0ʱ�����Ӹպ��ܾ���������ұ�Ե����� ![]()
���ӵļ��ٶȣ� ![]()
������ƫת�糡�е�ʱ�䣺 ![]()
����������ʽ��ã�
��U1=100V��
֪ƫת��ѹΪ100Vʱ������ǡ��������糡�����ٶ����
���ݶ��ܶ����ã� ![]()
�������ݽ�ã� ![]() m/s��
m/s��
����б�����Ϸ���б�����·�������ٶȷ����45��нǣ�
�𣺴�����������糡ʱ������ٶ�Ϊ1.41��105m/s��
��2���⣺����������糡�ٶȷ�����MN��н�Ϊ�ȣ���������糡ʱ�ٶȴ�СΪ�� ![]()
�������������ṩ��������qvB=m ![]()
��� ![]() ��
��
�����������ų���������ų�������Ϊ��
s=2Rsin��= ![]() m��
m��
�ɴ˿ɿ���������s�������ڴų��������ٶȵĴ�С�أ�sΪ��ֵ��
��֤���ԣ�����Ϊ0.4m��
��3���⣺�ɣ�1���н��ۿ�֪������������ų�����ֱ���ٶ�Խ�����ԽС���ʦ���СֵΪ��m=45�㣬
���龰��Բ����Ӧ��Բ�Ľ�Ϊ270�㣬���������ڴų��������ʱ��Ϊ��
![]() s
s
�����Ӵ��ϰ��Ե�ɳ��糡�ڽ���ų�ʱ���ڴų����˶���ʱ����̣�
![]() s��
s��
�������ڴų����˶����ʱ��Ϊ3�С�10��6s�����ʱ��Ϊ�С�10��6s��
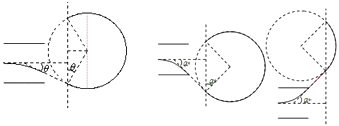
����������1�������ӴӼ�����ұ�Ե���ʱ�����ӵ��ٶ��������������ǿ�糡�е�ƫת��ͨ��ƫתλ�����ƫת�ĵ�ѹ����ͨ�����ܶ��������������糡ʱ������ٶȣ���2������������糡�ٶȷ�����MN��н�Ϊ�ȣ�������ƽ���˶��������糡ʱ���ٶ�����ٶȵĹ�ϵ���ٸ��ݴ��������ڴų���������Բ���˶�������뾶�ı���ʽ���Ӷ���������������ľ������ʽ�����Ƿ���нǦ��йأ���3�������������ڴų����˶���Բ�Ľ�����˶���ʱ�����Բ�Ľ���С��ʱ����̣���ƽ���˶���ֱ�����ϵķ��ٶ�Խ����������糡�ٶȷ�����MN��н�ԽС��Բ�Ľ�Խ���ݼ��ι�ϵ������Բ�ĽǺ���СԲ�Ľǣ�������������ڴų����˶����ʱ������ʱ�䣮

 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�