题目内容
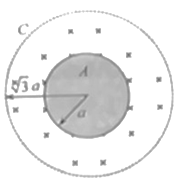
【题目】如图，半径为a的内圆A是电子发射器，其金属圆周表圆各处可沿纸面内的任意方向发射速率为v的电子；外圆C为与A同心的金属网，半径为
a。不考虑静电感应及电子的重力和电子间的相互作用，已知电子质量为m，电量为e。
(1)为使从C射出的电子速率达到3v，C、A间应加多大的电压U；
(2)C、A间不加电压，而加垂直于纸面向里的匀强磁场。
①若沿A径向射出的电子恰好不从C射出，求该电子第一次回到A时，在磁场中运动的时间t；
②为使所有电子都不从C射出，所加磁场磁感应强度B应多大。
【答案】（1）
（2）①
②
【解析】
（1）根据动能定理可求C、A间的电压；
（2）做出沿A径向射出的电子恰好不从C射出的轨迹，根据几何关系可求圆弧对应的圆心角，根据周期可求电子在在磁场中运动的时间；沿A切线射出的电子不从A射出，所有电子都不从C射出，做出轨迹，根据半径间的关系，结合电子在磁场中的半径，可求磁感应强度的最小值。
（1）对电子经C、A间的电场加速时，由动能定理得
得
（2）①电子在C、A间磁场中运动轨迹与金属网相切。轨迹如图所示：
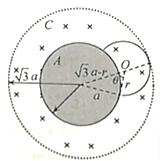
设此轨迹圆的半径为r，则
又T= 
得tanθ= 
故θ=60°
所以电子在磁场中运动的时间
得
②若沿切线方向射出的电子轨迹恰好与金属网C相切。则所有电子都不从C射出，轨迹如图所示：
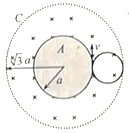
又
得B=
所以
练习册系列答案
阅读快车系列答案
相关题目
