题目内容
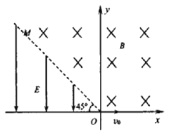
【题目】如图所示，在平面直角坐标系xoy的一、二象限内，分别存在以虚线OM为边界的匀强电场和匀强磁场。匀强电场方向沿y轴负方向，匀强磁场方向垂直于Xoy平面向里，虚线OM与x轴负方向成45°角。一质量为m、电荷量为+q的带电粒子从坐标原点O处以速度v0沿x轴正方向运动，粒子每次到x轴将反弹，第一次反弹无能量损失，以后每次反弹水平分速度不变、竖直分速度大小均减为反弹前的
、方向相反。电场强度大小等于
，磁感应强度大小等于
，求：(不计粒子重力，题中各物理量单位均为国际单位，计算结果可用分式表示)
(1)带电粒子第三次经过OM时的坐标；
(2)带电粒子第三次到达OM时经过的时间；
(3)带电粒子从第二次进入电场开始，沿电场方向运动的总路程。
【答案】(1) 
(2) 
(3) 
【解析】
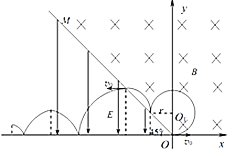
（1）设磁场强度大小为B，粒子进入磁场，根据左手定则，粒子做
的圆周运动后经过OM，根据洛伦兹力提供向心力，有：
，解得：
故第三次经过OM时的坐标为
；
（2）粒子在磁场中做圆周运动的周期为：
沿
轴方向加速度：
沿轴方向：
，
联立解得：
则带电粒子第三次到达OM时经过的时间为：
；
（3）因粒子第二次进入电场做类平抛运动，故到达
轴时的水平分速度为
竖直方向：
第一次竖直分速度减半反弹，竖直分速度
，高度：
第二次竖直分速度减半反弹，竖直分速度
，高度：
…….
第n次竖直分速度减半反弹，高度
故总路程为：
整理可以得到：
即带电粒子从第二次进入电场开始，沿电场方向运动的总路程为。
练习册系列答案
相关题目
