题目内容
【题目】如图所示,从地面离h1高处的空间,是可由某装置(图中未画出)控制的力作用区。当启动装置产生力作用区,小球在该区域的加速度即刻变为a=5g,方向始终向上;当关闭装置,小球在该区域可自由下落,现启动装置产生力作用区,并让小球从力作用区上方h2=20m处由静止释放,小球恰好能达到地面。取重力加速度g=10m/s2。
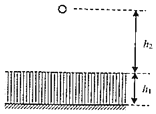
(1)求高度h1;
(2)若先将小球自地面上方h3=6m处由静止释放,再择机启动装置产生力作用区,小球能离开力作用区且不与地面接触,求小球从开始下落至第一次离开力作用区所经历的最长时间tm。
【答案】(1) h1=4m (2) t=1.6s
【解析】
(1)由小球恰好到达地面可知小球落地时速度为零,设小球到达力作用区时速度为v,
由运动学公式可知:
v2=2gh2
v2=2ah1
联立解得:h1=4m
(2)将小球自h3处释放,小球运动的最长时间对应小球恰好到达地面时速度为零,设在力作用区达到的最大速度为vm,下落过程中加速时间为t1,减速时间为t2,减速下落高度为h4,向上运动时间t3,
则由运动学公式可知:
vm2=2g(h3-h4)
vm2=2ah4
vm=gt1
vm=at2
![]()
经历的总时间为t=t1+t2+t3
联立解得:t=1.6s

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目