题目内容
【题目】“嫦娥四号”探月卫星发射后,先在“24小时轨道”上绕地球运行(即绕地球一圈需要24小时);然后,经过两次变轨依次到达“48小时轨道”和“72小时轨道”;最后奔向月球.如果按圆形轨道计算,并忽略卫星质量的变化,则在每次变轨完成后与变轨前相比
A.卫星线速度增大,角速度减小
B.卫星线速度减小,角速度减小
C.卫星动能减小,机械能减小
D.卫星动能减小,机械能增大
【答案】B
【解析】
万有引力提供向心力:
![]()
解得:
![]()
![]()
![]()
AB.根据题意两次变轨后,卫星分别为从“24小时轨道”变轨为“48小时轨道”和从“48小时轨道”变轨为“72小时轨道”,则由上式可知,在每次变轨完成后与变轨前相比运行周期增大,运行轨道半径增大,运行线速度减小,角速度减小,故A错误,B正确。
CD.每次变轨完成后与变轨前相比后,半径都增大,卫星必须点火加速,动能变大,机械能增大,故CD错误。

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
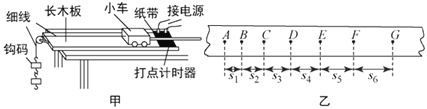
【题目】如图(甲)所示,研究平抛运动规律的实验装置放置在水平桌面上,利用光电门传感器和碰撞传感器可以测得小球的水平初速度v0和飞行时间t,底板上的标尺可以测得水平位移d.
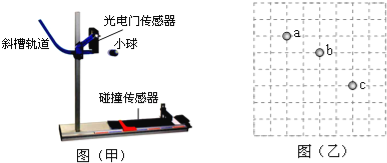
(1)控制斜槽轨道的水平槽口高度h不变,让小球从斜槽的不同高度处滚下,以不同的速度冲出水平槽口,以下说法正确的是
A.落地点的水平距离d与初速度v0成正比 |
B.落地点的水平距离d与初速度v0成反比 |
C.飞行时间t与初速度v0成正比 |
D.飞行时间t与初速度v0大小无关 |
(2)另一位同学做实验时,在装置的后面竖直放置一块贴有方格纸的木板,然后在方格纸上记录了小球某次平抛运动途经的三个位置a、b、c如图(乙)所示.该同学取下方格纸后,发现忘记记录水平和竖直方向了,已知小方格的边长L=1cm,则小球平抛运动的初速度可能为 .