题目内容
5.据报道,目前我国正在研制“萤火二号”火星探测器.探测器升空后,先在近地轨道上以线速度v环绕地球飞行,再调整速度进入地火转移轨道,最后再一次调整速度以线速度v′在火星表面附近环绕飞行,若认为地球和火星都是质量分布均匀的球体,已知火星与地球的半径之比为1:2,密度之比为5:7,设火星与地球表面重力加速度分别为g′和g,下列结论正确的是( )| A. | g′:g=4:1 | B. | g′:g=10:7 | C. | v′:v=$\sqrt{\frac{5}{28}}$ | D. | v′:v=$\sqrt{\frac{5}{14}}$ |
分析 在星球表面的物体受到的重力等于万有引力$G\frac{Mm}{{R}^{2}}=mg$,根据质量与密度的关系,代入化简可得出重力加速度与密度和半径的关系,进一步计算重力加速度之比.
根据根据牛顿第二定律有:$\frac{GMm}{{R}^{2}}=m\frac{{v}^{2}}{R}$和M=ρ•$\frac{4}{3}π{R}^{3}$化简解出速度的表达式,代入数据化简可得速度之比.
解答 解:AB、在星球表面的物体受到的重力等于万有引力$G\frac{Mm}{{R}^{2}}=mg$,
所以$g=\frac{GM}{{R}^{2}}=\frac{G•ρ•\frac{4}{3}π{R}^{3}}{{R}^{2}}=\frac{4}{3}πGρR$
所以$\frac{g′}{g}=\frac{ρ′}{ρ}•\frac{R′}{R}=\frac{5}{7}×\frac{1}{2}=\frac{5}{14}$,故AB错误.
CD、探测器绕地球表面运行和绕月球表面运行都是由万有引力充当向心力,
根据牛顿第二定律有:$\frac{GMm}{{R}^{2}}=m\frac{{v}^{2}}{R}$,得$v=\sqrt{\frac{GM}{R}}$ ①,M为中心体质量,R为中心体半径.
M=ρ•$\frac{4}{3}π{R}^{3}$ ②
由①②得:v=$\sqrt{\frac{4πGρ{R}^{2}}{3}}$
已知地球和火星的半径之比为1:2,密度之比为5:7,
所以探测器绕地球表面运行和绕月球表面运行线速度大小之比为:$\frac{v′}{v}=\sqrt{({\frac{R′}{R})}^{2}\frac{ρ′}{ρ}}=\sqrt{\frac{1}{4}×\frac{5}{7}}=\sqrt{\frac{5}{28}}$
故C正确、D错误.
故选:C.
点评 解决本题的关键掌重力等于万有引力这个关系,求一个物理量,我们应该把这个物理量先用已知的物理量表示出来,再根据表达式进行比较求解.

 图中为理想自耦变压器原理图,当a、b端加上33V交流电压时.c、d端电压Ucd=11V,若当c、b端加上33V交流电压时,则a、b端电压Uab为( )
图中为理想自耦变压器原理图,当a、b端加上33V交流电压时.c、d端电压Ucd=11V,若当c、b端加上33V交流电压时,则a、b端电压Uab为( )| A. | Uab=99V | B. | Uab=33V | C. | Uab=11V | D. | Uab=0V |
 如图所示,一水平导轨处于与水平方向成45°角向左上方的匀强磁场中,一根通有恒定电流l的金属棒,由于受到安培力作用而在粗糙的轨道上向右做匀速运动.现将磁场方向沿顺时针缓慢转动至竖直向上,在此过程中,金属棒始终保持匀速运动,已知棒与导轨间动摩擦因数为μ,且μ<1,则( )
如图所示,一水平导轨处于与水平方向成45°角向左上方的匀强磁场中,一根通有恒定电流l的金属棒,由于受到安培力作用而在粗糙的轨道上向右做匀速运动.现将磁场方向沿顺时针缓慢转动至竖直向上,在此过程中,金属棒始终保持匀速运动,已知棒与导轨间动摩擦因数为μ,且μ<1,则( )| A. | 金属棒所受摩擦力一直在减小 | B. | 导轨对金属棒的支持力一直在增大 | ||
| C. | 磁感应强度先变小后变大 | D. | 金属棒所受安培力恒定不变 |
| A. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{{r}_{2}}^{2}}{{{r}_{1}}^{2}}$ | B. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{r}_{1}}{{r}_{2}}$ | C. | $\frac{{ω}_{1}}{{ω}_{2}}$=$\sqrt{\frac{{r}_{1}}{{r}_{2}}}$ | D. | $\frac{{ω}_{1}}{{ω}_{2}}$=$\sqrt{\frac{{{r}_{2}}^{3}}{{{r}_{1}}^{3}}}$ |
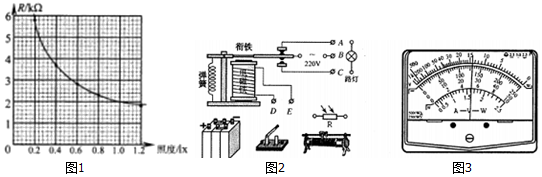
(1)某光敏电阻R在不同照度下的阻值如表,根据表中已知数据,在图1的坐标系中描绘出了阻值随照度变化的曲线.由图象可求出照度为1.0 x时的电阻约为2.0kΩ.
| 照度/1x | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 |
| 电阻/kΩ | 5.8 | 3.7 | 2.8 | 2.3 | 1.8 |
(3)用多用电表“×10Ω”档,按正确步骤测量图中电磁铁线圈电阻时,指针示数如图3所示,则线圈的电阻为140Ω,已知当线圈中的电流大于或等于2mA时,继电器的衔铁将被吸合.图中直流电源的电动势E=6V,内阻忽略不计,滑动变阻器有三种规格可供选择:R1(0-10Ω,2A)、R2(0-200Ω,1A)、R3(0-1750Ω,0.1A).要求天色渐暗照度降低至1.01x时点亮路灯,滑动变阻器应选择R3(填R1、R2、R3).为使天色更暗时才点亮路灯,应适当地减小(填“增大”或“减小”)滑动变阻器的电阻.
| A. | 安培发现了电流的磁效应 | |
| B. | 库仑通过扭秤实验发现了电流的热效应 | |
| C. | 奥斯特发现了磁场产生电流的条件和规律 | |
| D. | 麦克斯建立了电磁场理论并预言了电磁波的存在 |
| A. | 米、千克、牛顿等都是国际单位制中的基本单位 | |
| B. | 同一物体运动快时和运动慢时惯性一样大 | |
| C. | 静止在水平面上的物体所受的重力与水平面给的支持力是一对相互作用力 | |
| D. | 放在斜面上的物体,其重力沿垂直斜面的分力就是物体对斜面的压力 |
 “百公里加速时间”是衡量一辆跑车性能的重要指标,如图所示,某跑车在平直公路上由静止加速至108km/h只需要3.0s时间,已知跑车的质量为2000kg,加速和减速过程均可以视作匀变速直线运动.
“百公里加速时间”是衡量一辆跑车性能的重要指标,如图所示,某跑车在平直公路上由静止加速至108km/h只需要3.0s时间,已知跑车的质量为2000kg,加速和减速过程均可以视作匀变速直线运动.