��Ŀ����
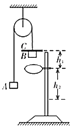
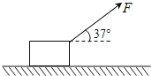
����Ŀ����ͼ,����M=1kg����������ˮƽ��ɦ�=37��ǵ�����F=10N�����£���ˮƽ����A�㾲ֹ��ʼ,�������ȼ���ֱ���˶�����֪AB����L=3m,���������Ķ�Ħ��������=0.5. (g=10m/s2,sin37��=0.6��cos37��=0.8)����
(1)�������˶��ļ��ٶȴ�С��
(2)���嵽��B����ٶȴ�С��
(3)��Ҫ�����Դ�A���ɾ�ֹ��ʼ�˶����ܵ���B��,��������F���õ����λ�ƴ�С
���𰸡���1��6m/s2��2��6m/s��3��1.36m
��������
��1������ţ�ٵڶ����������ٶȣ���2������v2=2aL������嵽��B��ʱ���ٶȣ���3��F����ʱ�����������˶�����ȥF�����ȼ����˶�������λ���ٶȹ�ϵ���F���õ���С����.
��1������ţ�ٵڶ����ɿɵã�![]()
���a=6m/s2
��2�������嵽��B��ʱ���ٶ�Ϊv����v2=2aL��
���v=6m/s
��3����F���õ���Сλ��Ϊx����ȥ����ǰ�ļ��ٶ�Ϊa=6m/s2����ȥ������ļ��ٶ�Ϊa�䣬���Mg=Ma��
���a��=5m/s2
�賷ȥ����ʱ������ٶ�v�䣬���У�v��2=2ax
v��2=2a��(L-x)
�������x��1.36m

��ϰ��ϵ�д�
�����Ŀ