题目内容
【题目】“阿特伍德机”是物理学家乔治阿特伍德在1784年研制的一种验证运动定律的机械。其基本结构为在跨过定滑轮的轻绳两端系着质量均为M的物块A和B,质量为m的金属片C放置在物块B上(不粘连)。铁架台上固定一圆环,圆环在物块B的正下方。系统静止时,金属片C与圆环间的高度差为h1。
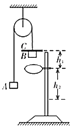
(1)由静止释放物块A、B,当物块B穿过圆环时,金属片C被搁置在圆环上,此后,物块B继续下落。如果忽略一切阻力,物块B穿过圆环后做______直线运动(选填“匀速”、“匀减速”或“匀加速”)。
(2)如果在实验误差允许的范围内,物块A、B和金属片C组成的系统,在下落h1高度的过程中,金属片C减少的重力势能等于系统增加的动能,即可验证该系统机械能守恒。测得物块B穿过圆环后下落h2高度所用时间为t,当地的重力加速度为g。则该系统机械能守恒的表达式为______。
(3)改变静止释放物块A、B的初始位置,重复试验,记录各次的高度差h1,以及物块B穿过圆环后下落相同高度h2所用的时间t,以h1为纵轴,以______为横轴(选填“![]() ”、“t2”或“
”、“t2”或“![]() ”),若作出的图线为一条过原点的直线,则说明了系统的机械能守恒。
”),若作出的图线为一条过原点的直线,则说明了系统的机械能守恒。
【答案】匀速 mgh1=![]()
![]()
【解析】
(1)因AB质量相同,则物块B穿过圆环后做匀速直线运动。
(2)由题意可知,系统ABC减小的重力势能转化为系统的增加的动能,即为:mgh+Mgh-Mgh=![]() (2M+m)v2,
(2M+m)v2,
即为:mgh1=![]() (2M+m)v2,又v=
(2M+m)v2,又v=![]()
得:mgh1=![]() (2M+m)(
(2M+m)(![]() )2
)2
(3)将mgh1=![]() (2M+m)v2,变形后,则有:
(2M+m)v2,变形后,则有:![]()
因此以![]() 为横轴;由上式可知,作出的图线是一条过原点的直线,直线的斜率k=
为横轴;由上式可知,作出的图线是一条过原点的直线,直线的斜率k=![]() 。
。

练习册系列答案
相关题目