Question

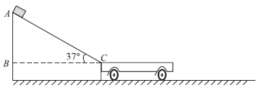
【题目】如图所示,有一块木板A静止在光滑且足够长的水平面上,木板质量M=4kg，长L=1.2m,木板右端放一小滑块B并处于静止,小滑块质量m=1kg,其尺寸远小于L小滑块与木板之间的动摩擦因数为μ=0.4(设最大静摩擦力等于滑动摩擦力,g=10m/s2)。

(1)现用恒力F始终作用在木板A上,为了让小滑块B不从木板A上滑落,求:恒力F大小的范围；

(2)其他条件不变,若恒力F大小为20.8N,且始终作用在木板A上,求:小滑块B滑离木板A时的速度大小；

(3)其他条件不变,若恒力F大小为28N,作用在木板A上一段时间后撒去,最终小滑块B从木板A上滑落下来,求:恒力F作用的最短时间。

Answer 1

【答案】（1）F≤20N（2）8m/s（3）

【解析】

（1）为了使小滑块B不从A上滑落，则AB两物体间的摩擦力等于最大静摩擦力，根据牛顿第二定律列式求解F的最大值；（2）当F=20.8N时，AB发生相对滑动，根据牛顿第二定律求出两者的加速度，根据位移关系求解B在A上滑行的时间，根据v=at求解B滑落时的速度；（3）先求撤去外力前后的加速度，结合v-t图像求解恒力F作用的最短时间.

（1）为了使小滑块B不从A上滑落，设A、B相对静止时的加速度为a，

对B有：ma≤μmg；对AB整体有：F=(M+m)a，

联立可得F≤20N；

（2）当F=20.8N时，AB发生相对滑动，此时B的加速度aB=μg.

设A的加速度为aA，有：F-μmg=MaA，

B在A上滑行的时间为t，有：

B滑落时的速度为v=aBt；

联立解得v=8m/s

（3）当外力F=28N，设撤去外力前A的加速度大小为aA′，有：

解得aA′=6m/s2，

设撤去外力F后A的加速度大小为 ，则，

解得

B从开始至与A共速期间加速度大小均为μg=4m/s2，设外力F作用的最短时间为t1，从开始到滑落所用的时间为t2，则AB物体对应的v-t图像如图；

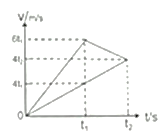
联立解得