��Ŀ����
����Ŀ����ͼ��ʾ��һ����Ϊm="1" kg��С����������ˮƽ�����˶��Ĵ��ʹ��ʵ�A�㣬�洫�ʹ��˶���B�㣬С����C����Բ�����߽�����ֱ�⻬�İ�Բ���ǡ����Բ���˶�����֪Բ���뾶R="0.9" m�������͵�ΪD�� D���ˮƽ��ĸ߶�h="0.8" m.С����뿪D���ǡ�ô�ֱ��������ˮƽ����E��Ĺ̶���б���壬��֪С����봫�ʹ���Ķ�Ħ������![]() =0.3�����ʹ���5m/s�㶨����˳ʱ��ת����g="10" m/2����
=0.3�����ʹ���5m/s�㶨����˳ʱ��ת����g="10" m/2����
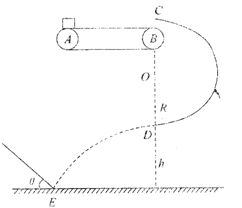
��1�����ʹ�AB���˵ľ��룻
��2��С��龭��D��ʱ�Թ����ѹ���Ĵ�С��
��3����б������ˮƽ���ļн���������ֵ��
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
�����������������(1)��С��飬��C����Բ�����߽�����ֱ�⻬�İ�Բ���ǡ����Բ���˶�����ţ�ٵڶ����ɵã�![]()
��![]() ��1�֣�
��1�֣�
��С����ڴ��ʹ���һֱ���٣���A��B��![]() ��1�֣�
��1�֣�
����![]() ��������ֵ��
��������ֵ��![]() (1�֣�
(1�֣�
(2)С����C��D���ɶ��ܶ���֪![]() (2�֣�
(2�֣�
��ţ�ٵڶ�����֪��D����![]() ��1�֣�
��1�֣�
������������ֵ��![]()
��ţ�ٵ������ɵ�С��龭��D��ʱ�Թ����ѹ����СΪ60 N��1�֣�
(3)С����뿪D�����ƽ���˶���![]() ��1�֣�
��1�֣�
(4)��С�����E����ٶȽ��зֽ��![]() 1�֣�
1�֣�
������������ֵ��![]() . ��1�֣�
. ��1�֣�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ