Question

【题目】如图，在一足够长的平直轨道上，某时刻质量m1＝0.12 kg的滑块甲以v1＝2.1 m/s的速度向右滑动，此时在甲正前方s0＝3.3 m处，质量为m2＝0.08 kg的滑块乙以v2＝1.5 m/s向左滑来，经过一段时间两滑块发生碰撞，碰后两滑块粘在一起，继续滑动一段距离静止在轨道上．两滑块与轨道之间的动摩擦因数均为μ＝0.03，g＝10 m/s2.如果两滑块相互作用的时间为t0＝0.02 s，甲、乙都可视为质点，则该过程产生的平均作用力分别为两滑块重力的多少倍？

Answer 1

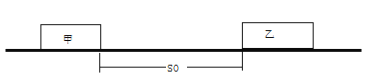
【答案】6m1g 9m2g

【解析】试题分析：应用牛顿第二定律与运动学公式求出碰撞前两滑块的速度，碰撞过程系统内力远大于外力，系统动量守恒，应用动量守恒定律求出碰撞后的速度，然后应用动量定理求出碰撞作用力。

假设两滑块从间距为s0＝3.3 m开始到发生碰撞所用的时间为t，

则由运动学公式：

由牛顿第二定律：μmg＝ma

可知两滑块的加速度大小为：a1＝a2＝μg＝0.3 m/s2

由以上各式可解得： t＝1 s　(t＝11 s舍去)

甲、乙两滑块碰前的速度大小分别为：

v′1＝v1－a1t＝1.8 m/s

v′2＝v2－a2t＝1.2 m/s

可知碰前的瞬间滑块甲的动量大于滑块乙的动量，则由动量守恒定律：

m1v′1－m2v′2＝(m1＋m2)v

解得：v＝0.6 m/s

对滑块甲由动量定理：Ft0＝m1(v－v′1)

代入数据解得：F＝－6m1g(负号表示F方向与甲运动方向相反)

对滑块乙由动量定理：F′t0＝m2(v－v′2)

代入数据解得：F′＝9m2g