Question

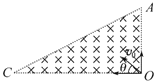
【题目】如图所示,质量为的带电小球用长为的绝缘细线（不可伸长）悬挂于点,并处在场强为. 水 平向左的匀强电场中，球静止时丝线与竖直方向的夹角.现将小球拉至虚线所示位置（细线水平拉直，与点高度相同）后由静止开始释放(,)。

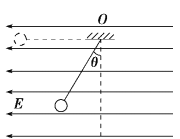
求：(1)小球带何种电荷，电荷量是多少？(2)小球摆动到最低点时速度的大小和细线所受拉力F的大小。

Answer 1

【答案】(1) ；(2)

【解析】

(1)小球静止在电场中时，受到重力、线的拉力和电场力而平衡，根据平衡条件确定小球的电性。小球在匀强电场中，受到的电场力大小为F=qE，根据平衡条件求出带电小球的电量；

(2)先由动能定理求出小球摆动到最低点时的速度v，再根据牛顿第二定律和向心力公式求解拉力FT的大小。

(1) 由于带电小球所受电场力方向向左，电场线方向也向左，则小球带正电。分析小球的受力情况，作出受力图如图，

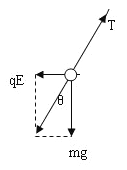
根据平衡条件得：

qE=mgtanθ

解得： ；

(2) 小球从水平位置摆动到最低点的过程中，由动能定理得：

解得：

小球在最低点时，由重力与细线的拉力的合力提供向心力，根据牛顿第二定律得：

解得：

由牛顿第三定律可知细线所受的拉力大小为。