题目内容
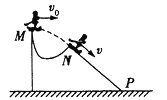
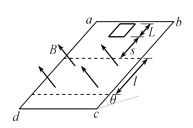
【题目】如图所示,在倾角为θ=30°的光滑绝缘斜面abcd上有一垂直斜面向上的匀强磁场,磁场的上下有边界且与斜面底边cd平行,虚线为磁场的边界线.在斜面上有一个质量为m=0.2kg、电阻为R=0.27Ω、边长为L=60cm的正方形金属线框,相距s=90cm.将线框从静止开始释放,沿斜面滑下,线框底边始终与斜面底边平行.若线框刚进入磁场时,恰好能做匀速运动.求:
(1)匀强磁场的磁感应强度B的大小;
(2)若线框的下边从进入磁场开始到离开磁场的时间为t=0.6s,磁场区域的宽度l为多少?
(3)若线框上边框穿出磁场前也已匀速运动,则线框在穿过磁场的整个过程中能产生多少的焦耳热.(重力加速度g=10m/s2)
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)线框进入磁场前沿斜面向下做匀加速直线运动,设底边刚进磁场时的速度为v,则
由动能定理得![]() mv2=mgssinθ得 v=3m/s
mv2=mgssinθ得 v=3m/s
线框底边切割磁感线产生的感应电动势E=BLv=IR
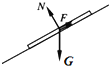
画出线框受力的侧视图如图所示.匀速运动,有:mgsinθ=BIL
联立解得:B=0.5T
(2)线框完全进入磁场后,磁通量不变,没有感应电流产生,线框不受安培力,而做匀加速运动,加速度为a=gsinθ=5m/s2
匀速运动的时间 t1=![]() =0.2s
=0.2s
匀加速运动的时间为:t2=t-t1=0.4s
匀加速运动的距离为:x=υt2+![]() at22=1.6m
at22=1.6m
磁场区域的宽度 l=L+x=2.2m
(3)上边框穿出磁场前也已匀速运动,则穿出磁场的速度仍为 v=3m/s
根据能量守恒可得 Q=mg(S+l+L)sinθ-![]() mv2=2.8J
mv2=2.8J

练习册系列答案
相关题目