题目内容
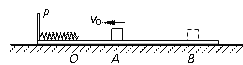
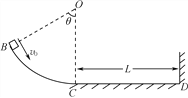
【题目】质量m＝1kg的小物块以初速度v0＝4m/s从B点沿切线方向进入光滑竖直的圆弧轨道BC.O点为圆弧的圆心，θ＝60°，轨道半径R＝0.8m，圆弧轨道与水平地面上长为L＝2.4m的粗糙直轨道CD平滑连接．小物块沿轨道BCD运动并与右侧的竖直墙壁发生碰撞．重力加速度取g＝10m/s2，空气阻力不计．求：
(1)小物块从B点运动到最低点C的过程中，重力做的功WG；
(2)小物块第一次经过最低点C时，圆弧轨道对物块的支持力FN；
(3)若小物块与墙壁碰撞后速度反向、大小变为碰前的一半，且只发生一次碰撞，那么小物块与轨道CD之间的动摩擦因数μ应该满足怎样的条件．
【答案】(1) WG＝4 J (2) FN＝40N (3)
【解析】(1)从B运动到C点过程中
，解得
(2)在最低点重力和支持力充当向心力，根据牛顿第二定可得：
根据动能定理可得
联立解得
(3)根据动能定理可得
，解得
，
，联立解得
综上得:
练习册系列答案
计算高手系列答案
相关题目
