Question

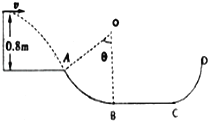
【题目】某游乐场的过山车从较高的弧形轨道顶部，由静止开始向下运动，在底部进入与之连接的圆形轨道，它可以底朝上在竖直圆轨道顶部运行，游客不会掉下来，可以把这种情形抽象为如图所示的简图，为了游客的安全，载人过山车在通过圆轨道的最高点时，对轨道要有一定的压力，假设该压力为人与过山车总重力的0.5倍，圆轨道的半径为R，不考虑一切阻力，问：

（1）载人过山车在最高点时的速度？

（2）弧形轨道顶部到底部的高度h应多大？

（3）若人的质量为m，过山车经过圆轨道最低点时人对座椅的压力多大？

Answer 1

【答案】(1) (2) (3)

【解析】

（1）在最高点时，由牛顿第二定律：

FN1=0.5Mg

解得；

（2）由机械能守恒：

解得

。

（3）由开始释放到最低点：

联立

FN2=6.5mg

牛三定律知

FN2＇=FN2=6.5mg