Question

【题目】长为L的轻杆可绕O在竖直平面内无摩擦转动，质量为M的小球A固定于杆端点，质点为m的小球B固定于杆中点，且M=2m，开始杆处于水平，由静止释放，当杆转到竖直位置时（ ）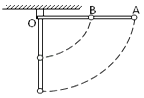

A.球A对轻杆做负功
B.球A在最低点速度为
C.OB杆的拉力小于BA杆的拉力
D.球B对轻杆做功 mgL

Answer 1

【答案】A,D
【解析】解：ABD、在转动过程中，A、B两球的角速度相同，设在最低点时A球的速度为vA，B球的速度为vB，则有vA=2vB

以A、B和杆组成的系统为研究对象，由机械能守恒定律，得

mg L+2mgL= mvB2+ 2mvA2．联立可以求出：vA= ，vB=

设杆对A、B两球作功分别为WA，WB．

根据动能定理得：

对A：2mgL+WA= 2mvA2

对B：mg L+WB= mvB2

解得：WA= mgL，WB=﹣ mgL，

可知杆对A球做正功，杆对B做负功，则球A对轻杆做负功，球B对轻杆做功为 mgL，AD符合题意，B不符合题意．C、当杆转到竖直位置时B的向心力向上，而向心力由B的合力提供，可知OB杆的拉力大于BA杆的拉力．C不符合题意．

故答案为：AD

两个小球角速度相等线速度之比等于半径之比，求解本题的隐含条件。