题目内容
【题目】静置于光滑水平面上的两相同滑块A与B紧靠在一起,长度均为L=1.25m,小滑块C静置于A的左端.已知C与A、B间的动摩擦因数均为μ=0.5,A、B、C质量均为m=1kg,现对C施加F=10N的水平恒力,将C从A的左端拉到B的右端的过程中,g取10m/s2 . 求:
(1)A对B做的功;
(2)B发生的位移大小.
【答案】
(1)
解:对C由牛顿第二定律有:
F﹣μmcg=mcac
代入数据解得ac=5m/s2
对AB整体由牛顿第二定律:
μmcg=(mA+mB)aA=2mAaA
当C运动到A右端时,有:
![]() (ac﹣aA)t12=L
(ac﹣aA)t12=L
此时A、B的速度为:
vB=vA=aAt1
联立代入数据解得vB=vA=2.5m/s,t1=1s,aA=2.5m/s2
对B,由动能定理得:
WAB= ![]() mvB2﹣0=
mvB2﹣0= ![]() =3.125J.
=3.125J.
C的速度:vc=act1=5×1m/s=5m/s
B的位移:xB1= ![]() aBt12=
aBt12= ![]() =1.25m
=1.25m
(2)
解:C进入B上滑动,A、B分离.C的加速度不变,对由牛顿第二定律:
μmcg=mBaB
当C从B左端运动到B右端时,有:
vct2+ ![]() act22﹣(vBt2+
act22﹣(vBt2+ ![]() aBt22)=L
aBt22)=L
x ![]() =vBt2+
=vBt2+ ![]() aBt2
aBt2
整个过程B的位移:xB=xB1+xB2
联立以上各式,代入数据解得:xB=3.125m
【解析】(1)根据牛顿第二定律求出C的加速度以及AB一起做匀加速直线运动的加速度,抓住C和A的位移之差等于L求出运动的时间,结合运动学公式求出滑块C滑上B时B的速度,结合动能定理求出A对B做功的大小.(2)根据位移时间公式求出C滑上B时,B的位移大小,C滑上B后,A与B脱离,根据牛顿第二定律和运动学公式求出B继续滑行的位移,从而得出B的总位移.
【考点精析】本题主要考查了匀变速直线运动的速度、位移、时间的关系和动能定理的理解的相关知识点,需要掌握速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值;动能定理的表达式是在物体受恒力作用且做直线运动的情况下得出的.但它也适用于变力及物体作曲线运动的情况;功和动能都是标量,不能利用矢量法则分解,故动能定理无分量式才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】图1为四缸发动机工作原理:内燃机通过连杆把四个汽缸的活塞连在一根曲轴上,并使各汽缸的做功过程错开,在飞轮转动的每半周里,都有一个汽缸在做功,其他三个汽缸分别在做吸气、压缩和排气工作.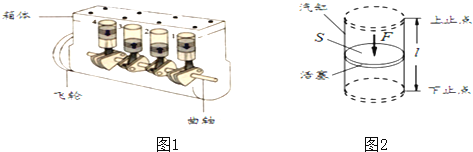
排量 | 2.0L |
输出功率 | 120kW |
转速 | 6000r/min |
(1)发动机在做功冲程里,高温、高压的燃气推动活塞向下运动,对外做功,同时将能转化为能.
(2)有一台四缸发动机,其主要技术指标如上表所示.其中排量等于四个汽缸工作容积的总和,汽缸工作容积指活塞从上止点到下止点所扫过的容积,又称单缸排量,它取决于活塞的面积和活塞上下运动的距离L(如图2).该发动机在1s内做功 J,单缸排量V=
L.