题目内容
【题目】有一如图所示的装置,轻绳上端系在竖直杆的顶端O点,下端P连接一个小球(小球可视为质点),轻弹簧一端通过铰链固定在杆的A点,另一端连接在P点,整个装置可以在外部驱动下绕OA轴旋转。刚开始时,整个装置处于静止状态,弹簧处于水平方向。现在让杆从静止开始缓慢加速转动,整个过程中,绳子一直处于拉伸状态,弹簧始终在弹性限度内,忽略一切摩擦和空气阻力。已知:OA=4m,OP=5m,小球质量m=1kg,弹簧原长l=5m,重力加速度g取10m/2。求:
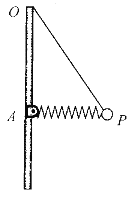
(1)弹簧的劲度系数k;
(2)当弹簧弹力为零时,整个装置转动的角速度ω。
【答案】(1)![]() (2)
(2)![]()
【解析】(1)开始整个装置处于静止状态,对小球进行受力分析,如图所示:
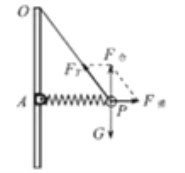
根据平衡条件得:![]()
![]() ,
,![]()
联立并代入数据解得:![]()
(2)当弹簧弹力为零时,小球上移至![]() 位置,绕
位置,绕![]() 中点C做匀速圆周运动,受力分析如图所示:
中点C做匀速圆周运动,受力分析如图所示:
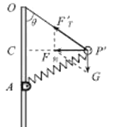
由图可得,轨道半径为![]() ,
,![]() ,其中
,其中![]()
根据牛顿第二定律得:![]()
联立解得:![]()

练习册系列答案
相关题目