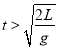题目内容
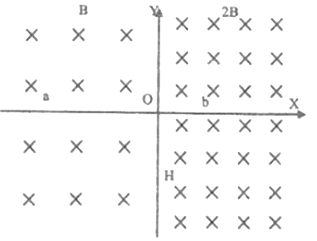
【题目】如图所示，在足够大的绝缘光滑水平桌面上建立平面直角坐标系，XOY坐标系内有垂直于桌面向下的范围足够大的匀强磁场，一、四象限内磁感应强度为2B，二、三象限内磁感应强度为B。现有a、b两个完全相同的金属小球，可视为质点，质量均为m，电量分别为+6q、-2q，分别从x轴上两点先后以垂直于x轴的水平速度射入第三和第四象限，其中b球入射速度为2v，a球第一次到达y轴时速度方向与y轴正向成60°角且恰好与第一次到达y轴的b球发生正碰，碰撞点记为H，碰后两球粘在一起继续运动，忽略两个小球之间的库仑力。求：
（1）a球第一次到达y轴所用时间；
（2）a球射入磁场时的速度大小；
（3）a、b球碰后第五次通过y轴所用时间及此时距碰撞点H的距离。
【答案】(1)
(2)3v(3)
；H点下方
处
【解析】
(1)经分析可知a球第一次到达Y轴时。速度偏转角为120°，即轨迹圆圆心角为120°，所用时间：
可得
④
可得
由①～⑤，可得
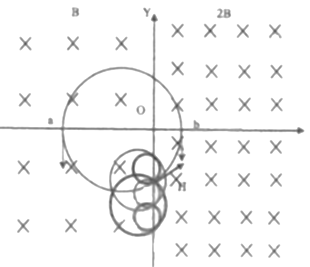
(2)经分析可知：a、b两球在H点相碰之前，做匀速圆周运动的轨迹圆半径
可得
(3)a、b两球在H点相碰前后，应用动量守恒定律
m3v-m2v=2mv共
解得
方向与Y轴正方向成60°角（即碰撞前瞬间a球的速度方向）
碰撞后，两个小球粘在一起，所带电量变为+4q
在第四象限内做匀速圆周运动时半径为
；
周期为
在第三象限内做匀速圆周运动时的半径为
周期为
由几何关系可知：
两球碰撞后，第五次次经过Y轴所用的时间
此时，两球在H点下方，距离为
练习册系列答案
相关题目
