题目内容
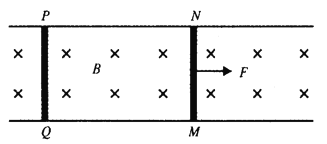
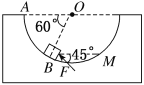
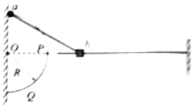
【题目】如图所示，左侧竖直墙面上固定不计为R=0.3m的光滑半圆环，右侧竖直墙面上与圆环的圆心O等高处固定一光滑直杆。质量为ma=2kg的小球a套在半圆环上，质量为mb=1kg的滑块b套在直杆上，二者之间用长为l=0.4m的轻杆通过两铰链连接。现将a从圆环的最高处由静止释放，使a沿圆环自由下滑，不计一切摩擦，a、b均视为质点，重力加速度g=10m/s2。求：
(1)小球a滑到与圆心O等高的P点时速度的大小；
(2)小球a从P点下滑至杆与圆环相切的Q点的过程中，杆对滑块b做的功；
(3)小球a从P点下滑至杆与圆环相切的Q点时，小球a与滑块b的速度之比.
【答案】(1)
；(2)
；(3)0.8.
【解析】
(1) 当a滑到与O同高度P点时，a的速度v沿圆环切线向下，b的速度为零，由机械能守恒定律可得
解得
代入数据解得
(2) (3)杆与圆相切时，如图所示，a的速度沿杆方向，设此时b的速度为vb，根据杆不可伸长和缩短，有
va=vbcosθ
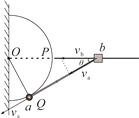
由几何关系可得
解得
在图中，球a下降的高度 h=Rcosθ，a、b系统机械能守恒，则有
对滑块b，由动能定理得
解得
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
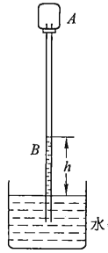
【题目】有一组同学对温度计进行了专题研究．他们通过查阅资料得知17世纪时伽利略曾设计过一个温度计，其结构为：一麦秆粗细的玻璃管，一端与一鸡蛋大小的玻璃泡相连，另一端竖直插在水槽中，并使玻璃管内吸入一段水柱．根据管中水柱高度的变化可测出相应的温度．为了研究“伽利略温度计”，同学们按照资料中的描述自制了如图所示的测温装置，图中A为一小塑料瓶，B为一吸管，通过软木塞与A连通，管的下端竖直插在大水槽中，使管内外水面有一高度差h，然后进行实验研究：
（1）在不同温度下分别测出对应的水柱高度h，记录的实验数据如下表所示．
温度 | 17 | 19 | 21 | 23 | 25 | 27 |
高度 | 30.0 | 24.9 | 19.7 | 14.6 | 9.4 | 4.2 |
| 5.1 | |||||
根据表中数据计算相邻两次测量水柱的高度差，并填入表内的空格．由此可得结论：①当温度升高时，管内水柱高度h将___________（选填“变大”“变小”或“不变”）．②水柱高度h随温度的变化而_________（选填“均匀”或“不均匀”）变化．试从理论上分析并证明结论②的正确性（提示：管内水柱产生的压强远远小于1个标准大气压）．______________．
（2）通过实验，同学们发现用“伽利略温度计”来测温度，还存在一些不足之外，其中主要的不足之处有：
①_______________________________．
②______________________________．
