题目内容
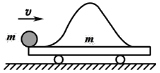
【题目】如图所示,空间存在竖直向下的匀强磁场,磁感应强度B=0.5T.在匀强磁场区域内,有一对光滑平行金属导轨,处于同一水平面内,导轨足够长,导轨间距L=1m,电阻可忽略不计。质量均为m=lkg,电阻均为R=2.5Ω的金属导体棒MN和PQ垂直放置于导轨上,且与导轨接触良好。先将PQ暂时锁定,金属棒MN在垂直于棒的拉力F作用下,由静止开始以加速度a=0.4m/s2向右做匀加速直线运动,5s后保持拉力F的功率不变,直到棒以最大速度vm做匀速直线运动.

(1)求棒MN的最大速度vm;
(2)当棒MN达到最大速度vm时,解除PQ锁定,同时撤去拉力F,两棒最终均匀速运动.求解除PQ棒锁定后,到两棒最终匀速运动的过程中,电路中产生的总焦耳热.
(3)若PQ始终不解除锁定,当棒MN达到最大速度vm时,撤去拉力F,棒MN继续运动多远后停下来?(运算结果可用根式表示)
【答案】(1)![]() (2)Q=5 J (3)
(2)Q=5 J (3)![]()
【解析】
(1)棒MN做匀加速运动,由牛顿第二定律得:F-BIL=ma
棒MN做切割磁感线运动,产生的感应电动势为:E=BLv
棒MN做匀加速直线运动,5s时的速度为:v=at1=2m/s
在两棒组成的回路中,由闭合电路欧姆定律得:![]()
联立上述式子,有:![]()
代入数据解得:F=0.5N
5s时拉力F的功率为:P=Fv
代入数据解得:P=1W
棒MN最终做匀速运动,设棒最大速度为vm,棒受力平衡,则有:![]()
![]()
代入数据解得:![]()
(2)解除棒PQ后,两棒运动过程中动量守恒,最终两棒以相同的速度做匀速运动,设速度大小为v′,则有:![]()
设从PQ棒解除锁定,到两棒达到相同速度,这个过程中,两棒共产生的焦耳热为Q,由能量守恒定律可得:![]()
代入数据解得:Q=5J;
(3)棒以MN为研究对象,设某时刻棒中电流为i,在极短时间△t内,由动量定理得:-BiL△t=m△v
对式子两边求和有:![]()
而△q=i△t
对式子两边求和,有:![]()
联立各式解得:BLq=mvm,
又对于电路有:![]()
由法拉第电磁感应定律得:![]()
又![]()
代入数据解得:![]()