题目内容
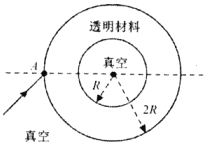
【题目】某种透明材料制成的空心球体外径是内径的2倍，其过球心的某截面(纸面内)如图所示。一束单色光(纸面内)从外球面上A点入射，入射角为45°时，光束经折射后恰好与内球面相切。
(1)求该透明材料的折射率；
(2)欲使光束从A点入射后，恰好在内球面上发生全反射，则应将入射角变为多少度?
【答案】（i）
（ii）30°
【解析】
（i）如答图，设光束经折射后到达内球面上B点在A点，由题意知，入射角i＝45°，折射角r＝∠BAO
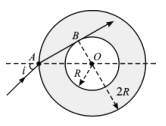
由几何关系有：sinr＝
＝0.5
由折射定律有：n＝
代入数据解得：n＝
（ii）如答图，设在A点的入射角为i'时，光束经折射后到达内球面上C点，并在C点恰发生全反射，则光束在内球面上的入射角∠ACD恰等于临界角C
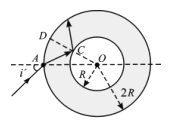
由sinC＝
代入数据得：∠ACD＝C＝45°
由正弦定理有
AO＝2R，CO＝R
解得：sin∠CAO＝
由折射定律有：n＝
解得：sini'＝0.5，即此时的入射角i'＝30°
练习册系列答案
阅读快车系列答案
相关题目
