��Ŀ����
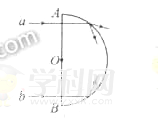
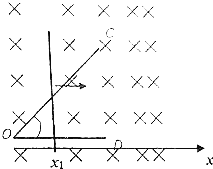
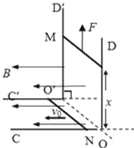
����Ŀ����ͼ���������l=0.4m��ƽ�н�������OC��O��C��ˮƽ���á����������Ҷ�O��O����������ˮƽ�洹ֱ�Ĺ⻬ƽ�е���OD��O��D���������뵼�촹ֱ�Ľ�����M��N�������ڵ����ϣ�����ʼ���뵼�챣�ֱ������õ�Ӵ���M��N��������Ϊm=0.2kg�������ΪR=0.4����N����ˮƽ�����Ķ�Ħ������Ϊ��=0.1�������ռ����ˮƽ�������ǿ�ų����Ÿ�Ӧǿ��ΪB=0.5T���ָ�N��һˮƽ����ij��ٶ�v0=3m/s��ͬʱ��M��һ��ֱ���������F��ʹM���ɾ�ֹ��ʼ���������ٶ�ΪaM=2m/s2���ȼ����˶���������費�ƣ���gȡ10m/s2������
(1)t=1sʱ��N����ͨ���ĵ���ǿ�ȴ�С��
(2)��M���»������У�����F��ʱ��t�ĺ�����ϵ�����涨��ֱ����Ϊ������
(3)��֪N��ֹͣ�˶�ʱ��M������ֱ����ϣ���M���˶���λ�ƣ�
(4)��N����ˮƽ�����˶�ֱ��ֹͣ�Ĺ����У���֪����F����Ϊ��11.1J����ϵͳ��������������
���𰸡���1��0.5A��2��F=1.6��0.1t��3��7.84m��4��2.344J
��������
(1)![]() �˵��ٶȣ�
�˵��ٶȣ�
![]()
��Ӧ������
![]()
(2)��![]() �ˣ�����ţ�ٵڶ����ɣ�
�ˣ�����ţ�ٵڶ����ɣ�
![]()
![]()
�����ã�
![]()
��ã�
![]()
(3)��![]() �ˣ���ţ�ٵڶ����ɵã�
�ˣ���ţ�ٵڶ����ɵã�
![]()
�ɵã�
![]()
��ã�
![]()
����![]() ͼ
ͼ
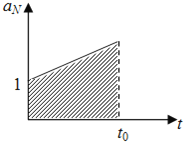
�ɵã�
![]()
��ã�
![]()
λ�ƣ�
![]()
(4)��![]() �ˣ����У�
�ˣ����У�
![]()
��ã�
![]()
��![]() �ˣ����У�
�ˣ����У�
![]()
��������
![]()

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�