题目内容
3.一物体做匀减速直线运动到停下,把整个运动分成三段,若使这三段运动的位移之比为1:2:3,通过这三段的平均速度之比$(\sqrt{6}+\sqrt{5}):(\sqrt{5}+\sqrt{3}):\sqrt{3}$.分析 首先采用逆向思维,将物体的运动看作反向的匀加速直线运动来处理;先根据x=$\frac{1}{2}a{t}^{2}$判断前3L、前5L、前6L的运动时间,再结合几何关系判断.
解答 解:物体做末速度为零的匀减速直线运动,将物体的运动看作反向的初速度为零的匀加速直线运动,根据$x=\frac{1}{2}a{t}^{2}$,有:t=$\sqrt{\frac{2L}{a}}$∝$\sqrt{L}$;
故对于初速度为零的匀加速直线运动,前3L、前5L、前6L的运动时间之比为$\sqrt{3}:\sqrt{5}:\sqrt{6}$,故对于正向的匀减速直线运动,通过这三段的时间之比为$(\sqrt{6}-\sqrt{5}):(\sqrt{5}-\sqrt{3}):\sqrt{3}$;
根据v=$\frac{x}{t}$,平均速度之比为$\frac{1}{{(\sqrt{6}-\sqrt{5})}}:\frac{2}{{(\sqrt{5}-\sqrt{3})}}:\frac{3}{{\sqrt{3}}}$=$(\sqrt{6}+\sqrt{5}):(\sqrt{5}+\sqrt{3}):\sqrt{3}$;
故答案为:$(\sqrt{6}+\sqrt{5}):(\sqrt{5}+\sqrt{3}):\sqrt{3}$.
点评 本题关键是采用逆向思维法,将末速度为零的匀减速直线运动看作反向的初速度为零的匀加速直线运动,然后灵活选择匀变速直线运动的公式进行分析.

练习册系列答案
相关题目
13. 如图所示,水平地面上放着一块木板,上面放一个木块,设木块对木板的压力为N,木块所受摩擦力为f.若使木块的B端逐渐升高时,A端不动,木块仍静止,则下列说法正确的是( )
如图所示,水平地面上放着一块木板,上面放一个木块,设木块对木板的压力为N,木块所受摩擦力为f.若使木块的B端逐渐升高时,A端不动,木块仍静止,则下列说法正确的是( )
 如图所示,水平地面上放着一块木板,上面放一个木块,设木块对木板的压力为N,木块所受摩擦力为f.若使木块的B端逐渐升高时,A端不动,木块仍静止,则下列说法正确的是( )
如图所示,水平地面上放着一块木板,上面放一个木块,设木块对木板的压力为N,木块所受摩擦力为f.若使木块的B端逐渐升高时,A端不动,木块仍静止,则下列说法正确的是( )| A. | N增大,f增大 | B. | N增大,f减小 | C. | N减小,f增大 | D. | N减小,f减小 |
2.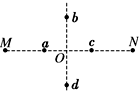 如图所示,真空中等量同种正点电荷放置在M、N两点,在MN的连线上有对称点a、c,MN连线的中垂线上有对称点b、d,则下列说法正确的是( )
如图所示,真空中等量同种正点电荷放置在M、N两点,在MN的连线上有对称点a、c,MN连线的中垂线上有对称点b、d,则下列说法正确的是( )
 如图所示,真空中等量同种正点电荷放置在M、N两点,在MN的连线上有对称点a、c,MN连线的中垂线上有对称点b、d,则下列说法正确的是( )
如图所示,真空中等量同种正点电荷放置在M、N两点,在MN的连线上有对称点a、c,MN连线的中垂线上有对称点b、d,则下列说法正确的是( )| A. | 正电荷+q在c点电势能大于在a点电势能 | |
| B. | 正电荷+q在c点电势能等于在a点电势能 | |
| C. | 在MN连线的中垂线上,O点电势最高 | |
| D. | 负电荷-q从d点静止释放,在它从d点运动到b点的过程中,加速度先减小再增大 |
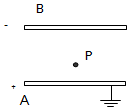 如图所示,已知平行板电容器两极板间距离d=5mm,充电后两极板电势差200V,A板带正电,若电容C=3μF,且P到B板的距离为3mm,求:
如图所示,已知平行板电容器两极板间距离d=5mm,充电后两极板电势差200V,A板带正电,若电容C=3μF,且P到B板的距离为3mm,求: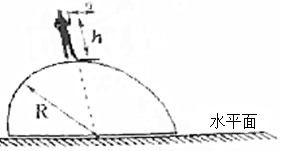 如图所示,一个人站在半径为R的半球形山包的最高点,将一小球以初速度v0水平抛出,小球抛出点离山包最高点距离为h,且h=R,已知重力加速度g=10m/s2,问:
如图所示,一个人站在半径为R的半球形山包的最高点,将一小球以初速度v0水平抛出,小球抛出点离山包最高点距离为h,且h=R,已知重力加速度g=10m/s2,问: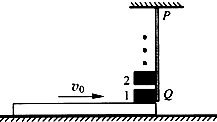 如图所示,光滑水平地面上有一足够长的木板,其质量M=5kg、以v0=7m/s的初速度沿水平地面向右运动.在木板的上方安装一个固定挡板PQ(挡板靠近但不接触木板),当木板的最右端到达挡板正下方时,立即将质量m=1kg的小铁块贴着挡板的左侧无初速地放在木板上,铁块与木板之间的动摩擦因数μ=0.5.当木板向右运动S=lm时,又无初速地贴着挡板在第1个小铁块上放置第2个相同的小铁块,以后每当木板向右运动lm就再放置一个相同的小铁块,直到木板停止运动(放到木板上的各个铁块始终被挡板挡住而保持静止状态,取g=10m/s2).求:
如图所示,光滑水平地面上有一足够长的木板,其质量M=5kg、以v0=7m/s的初速度沿水平地面向右运动.在木板的上方安装一个固定挡板PQ(挡板靠近但不接触木板),当木板的最右端到达挡板正下方时,立即将质量m=1kg的小铁块贴着挡板的左侧无初速地放在木板上,铁块与木板之间的动摩擦因数μ=0.5.当木板向右运动S=lm时,又无初速地贴着挡板在第1个小铁块上放置第2个相同的小铁块,以后每当木板向右运动lm就再放置一个相同的小铁块,直到木板停止运动(放到木板上的各个铁块始终被挡板挡住而保持静止状态,取g=10m/s2).求: ( 满偏电流100μA,内阻100Ω)
( 满偏电流100μA,内阻100Ω) (量程10mA,内阻40Ω)
(量程10mA,内阻40Ω) (最大电阻值100Ω)
(最大电阻值100Ω) (约300Ω)
(约300Ω) (电动势6V,内阻为几欧姆)
(电动势6V,内阻为几欧姆) 表示)和电流表
表示)和电流表