题目内容
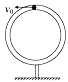
【题目】如图所示，一内壁光滑、质量为m、半径为r的环形细圆管(管的内径相对于环半径可忽略不计)用硬杆竖直固定在地面上。有一质量为m的小球可在圆管中运动(球直径略小于圆管直径，可看做质点)，小球以速率
经过圆管最高点时，恰好对管壁无压力，当球运动到最低点时，求硬杆对圆管的作用力大小为（ ）
A. 
B. 
C. 6mg D. 7mg
【答案】D
【解析】
从最高点到最低点，由机械能守恒定律解得达到最低点的速度，再由牛顿第二定律解得小球所受的支持力；对圆管及球整体列牛顿第二定律方程得解。
在最高点，球恰好对管壁无压力，则由重力提供向心力，故有：
，球运动到最低点过程，由于内壁光滑，机械能守恒，故有
，在最低点，由牛顿第二定律有
，联立解得
，以圆管为研究对象，由平衡条件得硬杆对圆管的作用力大小
。故选D。
练习册系列答案
互动英语系列答案
相关题目
