题目内容
18.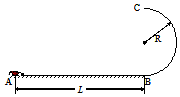 如图所示,一遥控电动赛车(可视为质点)从A点由静止以恒定的功率沿水平地面向右加速运动,当到达固定在竖直面内的光滑半圆轨道最低点B时关闭发动机,由于惯性,赛车继续沿半圆轨道运动,并恰好能通过最高点C(BC为半圆轨道的竖直直径).已知赛车的质量为m,半圆轨道的半径为R,A、B两点间的距离为1.5R,赛车在地面上运动时受到的阻力大小恒为$\frac{1}{3}mg$,不计空气阻力,重力加速度为g,下列判断正确的是( )
如图所示,一遥控电动赛车(可视为质点)从A点由静止以恒定的功率沿水平地面向右加速运动,当到达固定在竖直面内的光滑半圆轨道最低点B时关闭发动机,由于惯性,赛车继续沿半圆轨道运动,并恰好能通过最高点C(BC为半圆轨道的竖直直径).已知赛车的质量为m,半圆轨道的半径为R,A、B两点间的距离为1.5R,赛车在地面上运动时受到的阻力大小恒为$\frac{1}{3}mg$,不计空气阻力,重力加速度为g,下列判断正确的是( )| A. | 赛车通过C点后落回地面的位置到B点的距离为2R | |
| B. | 赛车通过B点时的速度大小为$2\sqrt{gR}$ | |
| C. | 赛车从A点运动到B点的过程中,其电动机所做的功为$\frac{5mgR}{2}$ | |
| D. | 要使赛车能滑过B点并沿半圆轨道滑回地面,其电动机所做的功W需满足的条件为$\frac{mgR}{2}<W≤\frac{3mgR}{2}$ |
分析 赛车恰好能通过最高点C时,由重力提供向心力,由此列式求出赛车通过C点时的速度.赛车离开C点后做平抛运动,由平抛运动的规律求赛车通过C点后落回地面的位置到B点的距离.从B到C的过程,由机械能守恒定律求赛车通过B点时的速度.研究赛车从A点运动到B点的过程,由动能定理求电动机所做的功.要使赛车能滑过B点并沿半圆轨道滑回地面,由动能定理和临界条件结合求电动机所做的功W需满足的条件.
解答 解:A、赛车恰好能通过最高点C时,由重力提供向心力,则有 mg=m$\frac{{v}_{C}^{2}}{R}$,得 vC=$\sqrt{gR}$
赛车离开C点后做平抛运动,则得:
水平方向有 x=vCt
竖直方向有 2R=$\frac{1}{2}g{t}^{2}$,解得 x=2R,即赛车通过C点后落回地面的位置到B点的距离为2R,故A正确.
B、从B到C的过程,由机械能守恒定律得:2mgR+$\frac{1}{2}m{v}_{C}^{2}$=$\frac{1}{2}m{v}_{B}^{2}$,解得 vB=$\sqrt{5gR}$.故B错误.
C、赛车从A点运动到B点的过程中,由动能定理得 W-$\frac{1}{3}$mg•1.5R=$\frac{1}{2}m{v}_{B}^{2}$,解得电动机做的功 W=3mgR.故C错误.
D、当赛车刚好运动到B点速度为零时,赛车从A点运动到B点的过程中,由动能定理得 W1-$\frac{1}{3}$mg•1.5R=0,解得电动机做的功 W1=$\frac{1}{2}$mgR
当赛车刚好能滑到与圆心等高处速度为零时,赛车从A点运动到与圆心等高位置的过程中,由动能定理得 W2-$\frac{1}{3}$mg•1.5R-mgR=0,解得电动机做的功 W2=$\frac{3}{2}$mgR,所以要使赛车能滑过B点并沿半圆轨道滑回地面,其电动机所做的功W需满足的条件为$\frac{mgR}{2}<W≤\frac{3mgR}{2}$.故D正确.
故选:AD
点评 解决本题的关键是要把握圆周运动的临界条件,知道赛车刚好通过C点时,重力等于向心力.刚好到达与圆心等高处时速度.分段运用动能定理研究.

 如图所示,一战斗机在距地面高度一定的空中,由东向西沿水平方向匀速飞行,发现地面目标P后,开始瞄准并投掷炸弹.若炸弹恰好击中目标P,假设投弹后飞机仍以原速度水平匀速飞行(空气阻力不计),则( )
如图所示,一战斗机在距地面高度一定的空中,由东向西沿水平方向匀速飞行,发现地面目标P后,开始瞄准并投掷炸弹.若炸弹恰好击中目标P,假设投弹后飞机仍以原速度水平匀速飞行(空气阻力不计),则( )| A. | 飞机投弹时在P点的正上方 | |
| B. | 炸弹落在P点时,飞机在P点的正上方 | |
| C. | 飞机飞行速度越大,投弹时飞机到P点的距离应越大 | |
| D. | 无论飞机飞行速度多大,从投弹到击中目标经历的时间是一定的 |
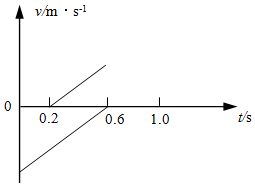 小球a从地面以一定的速度竖直向上抛出,经过一段时间后小球b从a的上方一定高度处由静止释放,最终两小球(均视为质点)同时落地.从a拋出的时刻开始计时,两小球在0~0.6s内的v-t图象如图所示.不计空气阻力,重力加速度g=10m/s2,下列判断正确的是( )
小球a从地面以一定的速度竖直向上抛出,经过一段时间后小球b从a的上方一定高度处由静止释放,最终两小球(均视为质点)同时落地.从a拋出的时刻开始计时,两小球在0~0.6s内的v-t图象如图所示.不计空气阻力,重力加速度g=10m/s2,下列判断正确的是( )| A. | 小球a抛出时的速率为6m/s | |
| B. | 小球b落地时的速率为8m/s | |
| C. | 从t=0时刻开始,a、b速率之差的绝对值先变小后变大 | |
| D. | t=0.6s 时,a、b间距为2.4m |
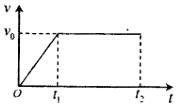 把一小物块轻轻放在一水平匀速运动的传送带的一端,物块一直运动到皮带另一端,其运动图象如图所示,图中所标的时间和速度以及重力加速度均为己知.下列说法正确的是( )
把一小物块轻轻放在一水平匀速运动的传送带的一端,物块一直运动到皮带另一端,其运动图象如图所示,图中所标的时间和速度以及重力加速度均为己知.下列说法正确的是( )| A. | 物块先受滑动摩擦力作用,后受静摩擦力作用 | |
| B. | 由图中的数据可求出皮带的长 | |
| C. | 由图中的数据可求出因摩擦产生的热量 | |
| D. | 由图中的数据可求出物块与皮带间的动摩擦因数 |
 如图所示,在光滑水平面上质量为m的物体A以速度v0与静止的物体B发生碰撞,物体B的质量为2m,则碰撞后物体B的速度大小可能为( )
如图所示,在光滑水平面上质量为m的物体A以速度v0与静止的物体B发生碰撞,物体B的质量为2m,则碰撞后物体B的速度大小可能为( )| A. | v0 | B. | $\frac{4}{3}$v0 | C. | 0 | D. | $\frac{{v}_{0}}{3}$ |
 如图,水平面上固定有形状为
如图,水平面上固定有形状为 的光滑金属导轨abcd和efgh;ab、ef平行,间距为2L;cd、gh平行,间距为L,且右端足够长;垂直ab 和ef 放置有质量为m 的粗细均匀金属棒MN,导轨cd、gh的最左端垂直放置另一质量也为m的金属棒PQ,两金属棒均与导轨接触良好.MN、PQ棒接入电路的电阻分别为2R 和R,导轨电阻不计.导轨平面内有垂直平面向外的匀强磁场,磁感应强度为B.现先将PQ棒固定,给MN棒一个水平向右大小为2v0的初速度,当MN棒速度减为v0时释放PQ 棒.当MN棒运动到导轨ab、ef的最右端时,回路中电流恰好为零.求:
的光滑金属导轨abcd和efgh;ab、ef平行,间距为2L;cd、gh平行,间距为L,且右端足够长;垂直ab 和ef 放置有质量为m 的粗细均匀金属棒MN,导轨cd、gh的最左端垂直放置另一质量也为m的金属棒PQ,两金属棒均与导轨接触良好.MN、PQ棒接入电路的电阻分别为2R 和R,导轨电阻不计.导轨平面内有垂直平面向外的匀强磁场,磁感应强度为B.现先将PQ棒固定,给MN棒一个水平向右大小为2v0的初速度,当MN棒速度减为v0时释放PQ 棒.当MN棒运动到导轨ab、ef的最右端时,回路中电流恰好为零.求:
 和
和 的面积分别为
的面积分别为 和
和 (
( ),初始时,甲车在乙车前方
),初始时,甲车在乙车前方 处,那么
处,那么
 ,两车不会相遇
,两车不会相遇 ,两车相遇2次
,两车相遇2次 ,两车相遇1次
,两车相遇1次 ,两车相遇1次
,两车相遇1次