题目内容
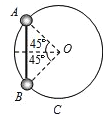
【题目】如图所示,半径为R的光滑圆环固定在竖直平面内,C是圆环最低点。两个质量均为m的小球A、B套在圆环上,用长为![]() R的轻杆相连,轻杆从竖直位置由静止释放,重力加速度为g,则下列说法正确的是( )
R的轻杆相连,轻杆从竖直位置由静止释放,重力加速度为g,则下列说法正确的是( )

A. B球到达C点时的速度大小为![]()
B. A球或B球在运动过程中机械能不变
C. 当轻杆到达水平位置时,A、B两球的速度相同,总动能最大
D. 轻杆最终能到达右侧竖直位置,然后返回
【答案】D
【解析】对于A、B组成的系统只有重力做功,系统的机械能守恒.B球运动到最低点C时,系统减小的重力势能为mg![]() R+mgR(1-
R+mgR(1-![]() )=mgR,由机械能守恒定律可得:
)=mgR,由机械能守恒定律可得: ![]() (2m)v2=mgR;解得:B球到达C点时的速度大小为 v=
(2m)v2=mgR;解得:B球到达C点时的速度大小为 v=![]() ;故A错误;
;故A错误;
因为杆子水平时,系统重力势能减小最大,根据系统的机械能守恒,知系统的总动能最大,但是两球的速度方向不同,即速度不同,故C错误;因A球或B球在运动中会受到杆的作用,杆的作用力对两个小球要做功,故单个小球的机械能不守恒;故B错误;由能量守恒关系可知,轻杆最终能到达右侧竖直位置,然后返回到原来位置,故选项D正确;故选D.

练习册系列答案
相关题目